Γρίφοι Υπολογισμού

Σύστημα εξισώσεων (**)

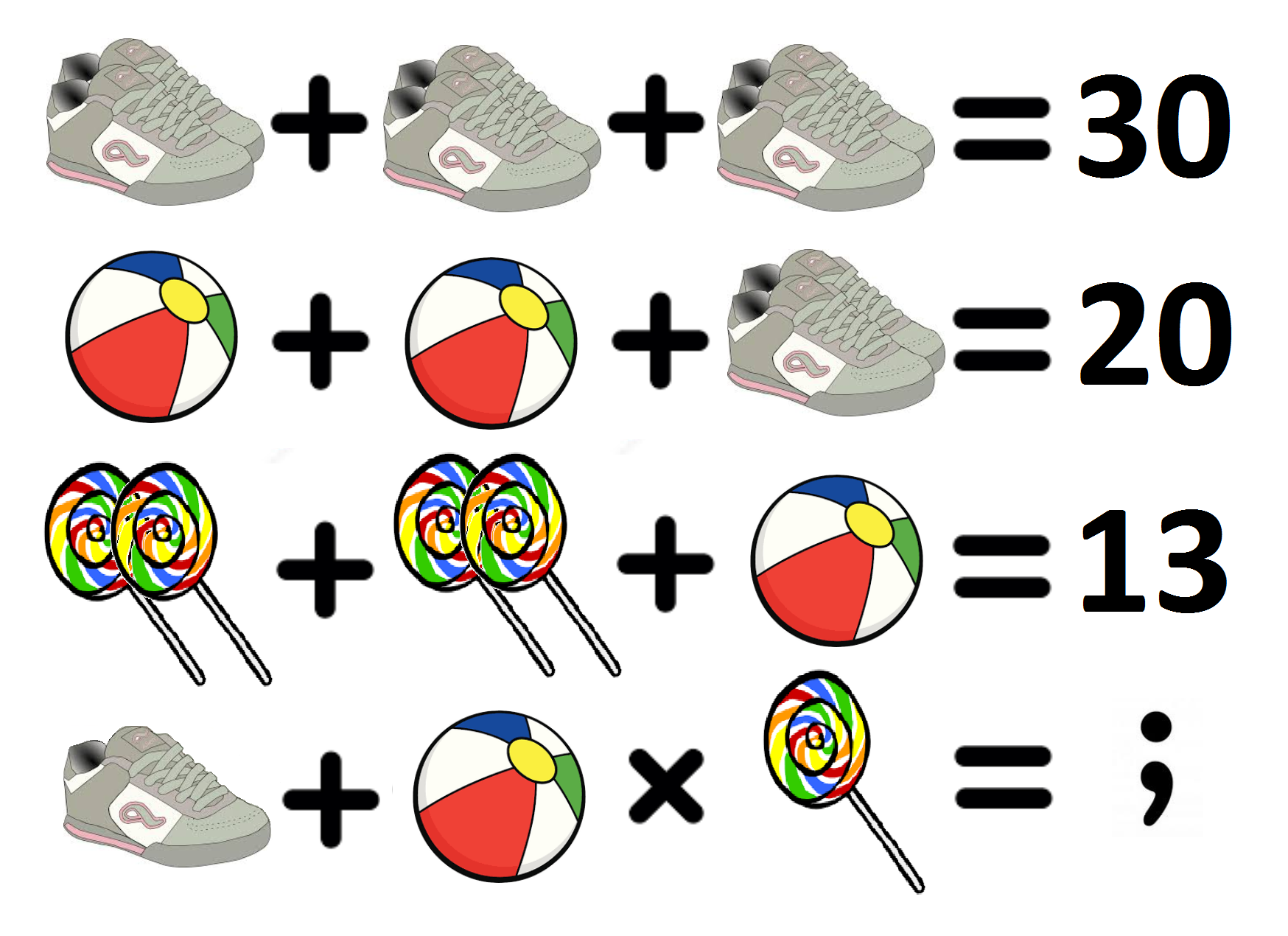
Το κάθε εικονιζόμενο σύμβολο αντιστοιχεί σε έναν αριθμό και με τις πράξεις ανάμεσά τους όλες οι εξισώσεις βγαίνουν σωστές. Ποιος αριθμός μπαίνει στη θέση του ερωτηματικού;

Λύση

Ένας φοιτητής έγραψε στον πίνακα την παρακάτω πράξη και ζήτησε να του πουν το αποτέλεσμα:

30-18÷3 = ;

Ένας συμφοιτητής του απάντησε 24, ενώ ο καθηγητής τους, που είχε μάλιστα PhD στα μαθηματικά, επέμενε πως το αποτέλεσμα είναι 4!
Έχει δίκιο ο καθηγητής;

Λύση

25 μυρμήγκια βρίσκονται σε 5 διαδοχικούς θαλάμους της φωλιάς τους, με διάταξη 5 μυρμηγκιών σε κάθε θάλαμο. Στόχος τους είναι να απλωθούν έτσι ώστε να βρίσκεται ένα μυρμήγκι σε κάθε θάλαμο. Υπάρχουν αρκετοί θάλαμοι τόσο αριστερά όσο και δεξιά αυτών που βρίσκονται ήδη. Χρειάζεται ένα λεπτό για να μετακινηθεί ένα μυρμήγκι στον διπλανό θάλαμο και κάθε λεπτό μετακινείται μόνο ένα μυρμήγκι. Πόση ώρα χρειάζονται για να επιτύχουν το στόχο τους;

Λύση

Ένα σκαθάρι ξεκινάει να κινείται κατά 1 μέτρο Ανατολικά, μετά 0,5 μέτρα Βόρεια, μετά 0,25 μέτρα Δυτικά, μετά 0,125 μέτρα Νότια και συνεχίζει την περίοδο κίνησης (Α-Β-Δ-Ν) μειώνοντας κάθε φορά την απόσταση που καλύπτει στο μισό της προηγούμενης. Στο τέλος της διαδρομής του ανακαλύπτει έναν μικρό σβόλο χώματος. Ποια ήταν η απόσταση του σβόλου από το σημείο εκκίνησης του σκαθαριού;

Λύση

Κάθε πέμπτος μαθηματικός είναι φιλόσοφος και κάθε ενδέκατος φιλόσοφος είναι μαθηματικός. Ποιοι είναι περισσότεροι, οι μαθηματικοί ή οι φιλόσοφοι;

Λύση

Σκεφτείτε έναν τριψήφιο αριθμό. Γράψτε στο κομπιουτεράκι σας αυτόν τον αριθμό δύο συνεχόμενες φορές. Π.χ. αν σκεφτήκατε τον αριθμό 123 γράψτε 123123. Διαιρέστε τον αριθμό που έχετε στην οθόνη σας με το 7. Θα παρατηρήσετε πως η διαίρεση είναι τέλεια, δηλαδή δεν προκύπτουν δεκαδικά ψηφία. Διαιρέστε τον νέο αριθμό που έχετε στην οθόνη σας με το 11. Πάλι η διαίρεση είναι τέλεια. Διαιρέστε τον νέο αριθμό με το 13. Και πάλι η διαίρεση είναι τέλεια και μάλιστα τώρα έχετε καταλήξει στον αρχικό σας αριθμό.
Μπορείτε να αποδείξετε ότι όλα τα παραπάνω ισχύουν για οποιονδήποτε τριψήφιο αριθμό;

Λύση

Το άθροισμα των ηλικιών δύο αδελφών είναι 11 έτη. Ο ένας είναι δέκα χρόνια μεγαλύτερος από τον άλλον. Ποιες είναι οι ηλικίες τους;

Λύση

Ένας άνθρωπος ζυγίζει 60 κιλά συν το ένα τρίτο του βάρους του. Πόσα κιλά ζυγίζει;

Λύση

Ένα μυρμήγκι έχει μπει μέσα σε ένα άδειο και κλειστό χαρτοκιβώτιο με διαστάσεις 40x30x20 εκατοστά. Βρίσκεται ακριβώς στη μία κορυφή του κουτιού και θέλει να περπατήσει μέχρι τη διαμετρικά απέναντι κορυφή, όπως φαίνεται στο σχήμα.

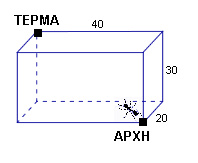
Ποιο είναι το μήκος της ελάχιστης διαδρομής που μπορεί να ακολουθήσει; Προσοχή γιατί υπάρχουν αρκετές επιλογές που δίνουν διαφορετικά μήκη διαδρομών.

Λύση

Συμβολίζουμε έναν τετραψήφιο αριθμό σαν ΑΒΓΔ που σημαίνει πως Α είναι οι χιλιάδες του, Β οι εκατοντάδες του, Γ οι δεκάδες του και Δ οι μονάδες του.
Βρείτε τα Α,Β,Γ,Δ που επαληθεύουν την ισότητα ΑΒΓΔ = 4 * ΔΓΒΑ

Λύση

Ο Κωστάκης έχει πάνω στο γραφείο του μία λωρίδα χαρτιού και προσπαθεί να τη διπλώσει στη μέση. Σηκώνει το δεξί άκρο της, το τσακίζει σε κάποιο σημείο που του φάνηκε κεντρικό και το διπλώνει πάνω στο αριστερό άκρο. Βλέπει όμως πως από τα αριστερά περισσεύουν 10 εκατοστά χαρτιού. Ξανανοίγει το χαρτί και πιάνει το αριστερό άκρο το τσακίζει σε ένα διαφορετικό σημείο και το διπλώνει πάνω στο δεξί άκρο. Όμως πάλι περισσεύουν 10 εκατοστά, αυτή τη φορά από τη δεξιά πλευρά του χαρτιού. Απογοητευμένος απλώνει τη λωρίδα χαρτιού στο γραφείο του που τώρα έχει πάνω της τα ίχνη από δύο τσακίσεις. Πόσα εκατοστά απέχουν αυτές οι δύο τσακίσεις μεταξύ τους;

Λύση

Το παρακάτω πρόβλημα πρωτοδημοσιεύθηκε στο βιβλίο του διάσημου φυσικού George Gamow "One, Two, Three, ..., Infinity" που κυκλοφόρησε το 1947, αλλά εκδίδεται ακόμα και σήμερα.
Ένας νεαρός ανακαλύπτει στο παλιό σεντούκι του παππού του έναν χάρτη θησαυρού. Ο χάρτης αναφέρει την τοποθεσία ενός έρημου νησιού και τις παρακάτω οδηγίες για την ανεύρεση ενός θησαυρού που είναι θαμμένος σε αυτό: "Στο νησί υπάρχει μια βελανιδιά, ένα πεύκο και έχουν στήσει και μια αγχόνη. Ξεκίνα από την αγχόνη και περπάτα ίσια προς τη βελανιδιά μετρώντας τα βήματά σου. Μόλις φτάσεις στη βελανιδιά στρίψε δεξιά, σχηματίζοντας ορθή γωνία με την προηγούμενη διαδρομή σου και περπάτησε τον ίδιο αριθμό βημάτων. Κάρφωσε έναν πάσσαλο στο σημείο αυτό. Γύρνα πίσω στην αγχόνη και ξεκινώντας πάλι από αυτήν, περπάτα προς το πεύκο μετρώντας τα βήματά σου. Στο πεύκο στρίψε αριστερά, σχηματίζοντας πάλι ορθή γωνία και περπάτα τον ίδιο αριθμό βημάτων που έκανες από την αγχόνη μέχρι το πεύκο. Κάρφωσε έναν πάσσαλο στο σημείο αυτό. Σκάψε στα μισά του δρόμου ανάμεσα στους δύο πασσάλους και θα βρεις εκεί τον θησαυρό".
Όλο ενθουσιασμό ο νεαρός φτάνει στο νησί, βλέπει τη βελανιδιά και το πεύκο, αλλά πουθενά η αγχόνη. Μάλλον την είχαν μεταγενέστερα αφαιρέσει και το ίχνος όπου βρισκόταν έχει εξαφανισθεί. Πώς μπορεί ο νεαρός να βρει το ακριβές σημείο που είναι θαμμένος ο θησαυρός χωρίς το στίγμα της αγχόνης;

Λύση

Το κλαμπ των Μαθηματικών αριθμεί 500 μέλη, εκ των οποίων κάποια είναι παλιά και κάποια καινούργια (έχουν γραφτεί μέσα στον τελευταίο χρόνο). Αποφάσισε να διοργανώσει μία εκδήλωση για την οποία το κάθε παλιό μέλος θα πληρώσει συμμετοχή 20 ευρώ, ενώ το κάθε νέο μέλος θα πληρώσει 14 ευρώ. Η εκδήλωση πραγματοποιήθηκε και ενώ ήρθαν όλα τα νέα μέλη του κλαμπ, από τα παλιά μέλη συμμετείχε μόνο το 70%. Πόσα χρήματα συγκεντρώθηκαν στο ταμείο του κλαμπ από αυτήν την εκδήλωση;

Λύση

Συμβολίζουμε έναν διψήφιο αριθμό σαν ΑΒ, που σημαίνει πως το Β είναι οι μονάδες και το Α οι δεκάδες του. Να βρεθούν τα Α, Β και Γ, όπου Α > 0, για τα οποία ισχύει η ισότητα ΑΒ * ΑΒ = ΓΑΒ. Για παράδειγμα αν ίσχυε η ισότητα 14 * 14 = 614, τότε θα είχαμε Γ=6, Α=1, Β=4, αλλά προφανώς η ισότητα αυτή δεν ισχύει. Υπάρχει μία λύση για την οποία το Γ είναι μονοψήφιος αριθμός και μία λύση για την οποία το Γ είναι διψήφιος αριθμός (ο συνολικός αριθμός ΓΑΒ δηλαδή έχει 4 ψηφία). Προσπαθήστε να τις βρείτε και τις δύο χωρίς να δοκιμάσετε όλους τους πιθανούς συνδυασμούς.

Λύση

Έχουμε ένα χαλασμένο ρολόι το οποίο χάνει 24 λεπτά κάθε ώρα. Το ρυθμίσαμε στις 12:00 το μεσημέρι να δείχνει τη σωστή ώρα και τώρα δείχνει 3:00. Σταμάτησε όμως να λειτουργεί εδώ και μία ώρα. Τι ώρα είναι τώρα;

Λύση

Η μητέρα είναι 21 χρόνια μεγαλύτερη από το παιδί της. Σε 6 χρόνια η μητέρα θα έχει την πενταπλάσια ηλικία από την ηλικία που θα έχει τότε το παιδί της. Που βρίσκεται τώρα ο πατέρας;
Υπόδειξη: Η απάντηση προκύπτει αν προσεγγίσετε το πρόβλημα μαθηματικά.

Λύση

Από την κορυφή δύο τηλεφωνικών στύλων ύψους 10 μέτρων ο καθένας, κρέμεται ένα καλώδιο μήκους 15 μέτρων που τους συνδέει. Ένας τεχνικός του ΟΤΕ μετράει την απόσταση του χαμηλότερου σημείου του καλωδίου από το έδαφος και βρίσκει πως είναι 2,5 μέτρα. Πόσο απέχουν οι δύο στύλοι μεταξύ τους;

Λύση

Ένας σύλλογος έχει αναλάβει να διοργανώσει ένα τουρνουά πινγκ-πονγκ. Οι αγώνες είναι νοκ-άουτ, που σημαίνει πως όποιος χάνει δεν ξανα-αγωνίζεται, ενώ δεν υπάρχει περίπτωση ισοπαλίας μεταξύ των δύο αθλητών. Όποιος κερδίσει προκρίνεται στον επόμενο γύρο, μέχρι τελικά να αναδειχθεί ένας νικητής. Δεν γίνονται αγώνες για την 3η, 4η, κλπ. θέση.
Ο υπεύθυνος του τουρνουά θέλει να μπορεί να υπολογίσει γρήγορα τον ελάχιστο συνολικό αριθμό των αγώνων που θα απαιτηθούν για την ανάδειξη ενός νικητή ώστε να κανονίσει το πρόγραμμα της διοργάνωσης. Και για να το επιτύχει αυτό θα πρέπει να ξέρει εκ των προτέρων έναν τύπο υπολογισμού του αριθμού των αγώνων που απαιτούνται, αν δηλώσουν συμμετοχή x αθλητές.
Μπορείτε να του υποδείξετε τον τύπο αυτόν; Και το σημαντικότερο: μπορείτε να τον πείσετε με λογικά επιχειρήματα ότι έχετε δίκιο;

Λύση

Πρόσφατα εγκαταστάθηκε ένα καλώδιο με οπτικές ίνες που περικλείει κυκλικά τη Γη στο επίπεδο του εδάφους και κατά μήκος του ισημερινού της. Το καλώδιο διέρχεται τυχαία μέσα από ένα ορνιθοτροφείο στο Εκουαδόρ, αλλά τα κοτόπουλα του ορνιθοτροφείου δυστυχώς αρνούνται να περάσουν από πάνω του. Ο πτηνοτρόφος διαμαρτυρήθηκε στην τηλεπικοινωνιακή εταιρεία και αυτή έστειλε αμέσως έναν τεχνικό για να δώσει λύση στο πρόβλημα. Αυτός πρότεινε να ανυψωθεί το καλώδιο από το έδαφος κατά ένα μέτρο ώστε να μπορούν τα κοτόπουλα να περνούν από κάτω. Για τεχνικούς όμως λόγους, αν γίνει αυτό στην περιοχή του ορνιθοτροφείου, θα πρέπει να γίνει το ίδιο και σε όλες τις θέσεις από τις οποίες διέρχεται το καλώδιο, δηλαδή σε όλο το γύρο της Γης. Η εταιρεία δέχθηκε να πληρώσει το κόστος όλων των απαραίτητων υποστυλώσεων, με την προϋπόθεση πως ο πτηνοτρόφος θα πληρώσει το επιπλέον καλώδιο που θα χρειαστεί, με κόστος μισό ευρώ ανά μέτρο καλωδίου.
Μπορεί ο πτηνοτρόφος να δεχθεί μια τέτοια συμφωνία από οικονομικής άποψης;

Λύση

Ένας μετεωρολόγος μετράει κάθε μέρα και επί πέντε μέρες τη θερμοκρασία σε βαθμούς Κελσίου κάποιου σημείου μιας πόλης και βρίσκει 5 διαφορετικές θερμοκρασίες, στρογγυλοποιημένες σε ακέραιους αριθμούς. Παρατηρεί επίσης ότι το γινόμενο αυτών των 5 διαφορετικών θερμοκρασιών είναι ο αριθμός 12. Ποιες θερμοκρασίες μέτρησε;

Λύση

Ανάμεσα στις πόλεις Α και Ε παρεμβάλλεται ένα βουνό. Ο δρόμος που συνδέει τις δύο πόλεις αποτελείται από μία ευθεία 60 χιλιόμετρα (ΑΒ στο σχήμα), μία ανηφόρα 30 χιλιόμετρα (ΒΓ), μία κατηφόρα 30 χιλιόμετρα (ΓΔ) και μία ευθεία 60 χιλιόμετρα (ΔΕ). Ενα αυτοκίνητο πηγαίνει από την πόλη Α στην πόλη Ε και τρέχει ως εξής: στο κομμάτι ΑΒ τρέχει με 60 χ.α.ω. (τη μέγιστη του αυτοκινήτου σε φυσιολογικές συνθήκες όπως η ευθεία), στο κομμάτι ΒΓ με 30 χ.α.ω. (λόγω της ανηφόρας) και στο κομμάτι ΔΕ επίσης με 60 χ.α.ω.
Με τι ταχύτητα πρέπει να τρέξει το αυτοκίνητο στην κατηφόρα ΓΔ (όπου λόγω της κατηφόρας μπορεί να αναπτύξει μεγαλύτερη ταχύτητα από την μέγιστη του), ώστε να κάνει την διαδρομή ΑΒΓΔΕ με μέση ταχύτητα 60 χ.α.ω. (χιλιόμετρα ανά ώρα) ;

Λύση

Ένας μικρός ξυπνάει το πρωί για να πάει σχολείο. Καθώς έφτιαχνε τη σάκα του κοιτάζει βιαστικά από τον καθρέφτη του δωματίου του ένα ρολόι δεικτών που βρισκόταν στο χωλ και βλέπει μια ώρα που δεν μπορεί να ήταν σωστή, οπότε υπέθεσε λανθασμένα πως το ρολόι ήταν σταματημένο. Ανεβαίνει στο ποδήλατό του και μετά από 20 λεπτά ακριβώς φτάνει στο σχολείο του. Το ρολόι του σχολείο έδειχνε δύο ώρες και τριάντα λεπτά μετά από την ώρα που είδε στον καθρέφτη του σπιτιού του.
Τι ώρα έφτασε στο σχολείο;

Λύση

Εχουμε ένα φορτηγό με 10 τόνους καρπούζια. Το κάθε καρπούζι αποτελείται από νερό σε ποσοστό 99% επί του βάρους του. Το φορτηγό μένει πολλή ώρα στον ήλιο και εξατμίζεται μια ποσότητα νερού. Έτσι λόγω της εξάτμισης το κάθε καρπούζι αποτελείται τώρα κατά 98% από νερό (αντί 99% που ήταν πριν). Πόσο ζυγίζουν τώρα τα καρπούζια;

Λύση

Μια εταιρία χρησιμοποίησε 20 εργάτες επί 6 μήνες, εργαζόμενους 8 ώρες το 24ωρο, για να τελειώσει το μισό ενός έργου. Επειδή το υπόλοιπο του έργου πρέπει να τελειώσει σε 2 μήνες, η εταιρία αποφάσισε να προσλάβει και άλλους εργάτες, της ίδιας απόδοσης ανά ώρα, οι οποίοι θα δουλεύουν επί 10 ώρες το 24ωρο, ενώ οι υπάρχοντες εργάτες θα δουλεύουν όπως και πριν. Πόσους επιπλέον εργάτες πρέπει να προσλάβει η εταιρία ώστε να τελειώσει το έργο ακριβώς σε δύο μήνες;

Λύση

Σε ένα Συνέδριο Μαθηματικών ρωτήθηκε ένας ομιλητής ποια είναι η ηλικία του. Εκείνος απάντησε: Το τετράγωνο της ηλικίας μου είναι το έτος γέννησής μου. Αν ο μαθηματικός αυτός ζει ακόμα, πότε έγινε το Συνέδριο;

Λύση

Ο Δήμος της Αθήνας προσέλαβε τον Αρη και τον Βασίλη να βάψουν τις κολώνες ενός κεντρικού δρόμου. Υπάρχει ίσος αριθμός κολωνών και στις δύο πλευρές του δρόμου, γι αυτό αποφάσισαν να βάψει ο Αρης τις κολώνες της μίας πλευράς και ο Βασίλης της άλλης.
Ο Αρης έπιασε δουλειά πρωί-πρωί, ενώ ο Βασίλης ήρθε καθυστερημένος και όταν έφτασε, ο Αρης είχε βάψει ήδη 3 κολώνες. Ο Βασίλης που προτιμούσε να βάψει την πλευρά που άρχισε ο Αρης, τον παρακάλεσε να τον αφήσει να συνεχίσει αυτός από την 4η κολώνα και να ξεκινήσει ο Αρης να βάφει από την αρχή στην άλλη πλευρά. Ο Αρης δέχτηκε και άλλαξε πλευρά. Ο Βασίλης τελείωσε πιο γρήγορα και έτσι βοήθησε τον Αρη, βάφοντάς του 6 κολώνες από τη δική του πλευρά.
Ποιος από τους δύο έβαψε περισσότερες κολώνες και πόσες περισσότερες;

Λύση

Ένας κύριος επιστρέφει σπίτι με το σκύλο του, μετά από βόλτα που τον είχε βγάλει. Ο κύριος περπατάει με σταθερή ταχύτητα 4 χιλιομέτρων την ώρα. Επειδή ο σκύλος του ήταν πολύ ανήσυχος, 8 χιλιόμετρα πριν φτάσουν, του αφήνει το λουρί για να τρέξει σπίτι. Ο σκύλος τρέχει με σταθερή ταχύτητα 10 χιλιομέτρων την ώρα. Μόλις φτάνει στο σπίτι και βλέπει την πόρτα κλειστή, κάνει ακαριαία μεταβολή και επιστρέφει με την ίδια ταχύτητα προς το αφεντικό του. Μόλις τον φτάσει κάνει πάλι μεταβολή και ξανακατευθύνεται προς το σπίτι. Αυτό το μπρος-πίσω του σκύλου επαναλαμβάνεται μέχρι που φτάνει ο κύριος στο σπίτι και του ανοίγει την πόρτα. Πόση απόσταση θα έχει διανύσει ο σκύλος από τη στιγμή που του άφησε το λουρί;
Υπόδειξη: Οι φυσικοί λύνουν αυτό το πρόβλημα πιο γρήγορα από τους μαθηματικούς ;-)

Λύση

Μια γνωστή σοκολατοβιομηχανία σκέφτηκε την ακόλουθη προσφορά για να διαφημίσει τα προϊόντα της: Κάθε επτά χαρτιά περιτυλίγματος της σοκολάτας τους που θα τους έφερνε κάποιος, θα του έκαναν μία σοκολάτα δώρο. Ένας μικρός μέτρησε τα χαρτιά από τις σοκολάτες που είχε φάει και τα έβγαλε 49. Πόσες σοκολάτες δικαιούται να πάρει δωρεάν;

Λύση

Ο Πέτρος και η Μαρία ζουν μαζί με τα 12 παιδιά τους. Κάποια από αυτά είναι από τον προηγούμενο γάμο του Πέτρου και κάποια από τον προηγούμενο γάμο της Μαρίας. Ο καθένας τους συνδέεται άμεσα με 9 από τα παιδιά αυτά. Πόσα παιδιά απέκτησαν μαζί;

Λύση

Ένας τοξότης έχει ένα τόξο και εξήντα βέλη. Αν ρίξει το πρώτο του βέλος στις 12:00 το μεσημέρι και συνεχίσει να ρίχνει ένα βέλος κάθε λεπτό, τι ώρα θα του τελειώσουν τα βέλη;

Λύση

Ένας επιχειρηματίας ανακοίνωσε στους υπαλλήλους του ότι όποιος συμπληρώσει 8 καθαρές ώρες εργασίας στο ταμείο της εταιρίας, θα πάρει προαγωγή! Η μόνη προϋπόθεση που έθεσε ήταν ότι δεν επιτρέπεται να εργασθούν στο ταμείο κάθε μέρα περισσότερο από το μισό του χρόνου που τους απομένει για να συμπληρώσουν αυτές τις 8 ώρες. Την πρώτη μέρα δηλαδή ένας υπάλληλος μπορεί να εργασθεί στο ταμείο μέχρι 4 ώρες, τη δεύτερη μέχρι 2, κ.ο.κ. Σε πόσες ημέρες ένας εργατικός υπάλληλος θα καταφέρει να πάρει την προαγωγή;

Λύση

Ένα νούφαρο βρίσκεται στο κέντρο μιας λίμνης και κάθε μέρα διπλασιάζει το μέγεθός του. Σε 10 μέρες έχει καλύψει όλη τη λίμνη. Σε πόσες μέρες είχε καλύψει τη μισή λίμνη;

Λύση

Ο Ανδρέας και ο Βασίλης έτρεξαν σε μια κούρσα 100 μέτρων. Όταν ο Ανδρέας τερμάτισε, ο Βασίλης βρισκόταν στα 90 μέτρα. Ο Ανδρέας πρότεινε στον Βασίλη να ξανατρέξουν αλλά αυτή τη φορά θα ξεκινούσε 10 μέτρα πριν τη γραμμή εκκίνησης για να είναι πιο αμφίρροπο το αποτέλεσμα. Αν κρατηθούν όλες οι άλλες συνθήκες ίδιες, θα κερδίσει ο Ανδρέας, ο Βασίλης ή θα τερματίσουν ταυτόχρονα;

Λύση

Ένα σκουλήκι ξεκινάει να σκαρφαλώσει κάθετα σε έναν τοίχο ύψους 20 μέτρων. Τη μέρα που είναι φρέσκο ανεβαίνει 3 μέτρα, αλλά τη νύχτα που νυστάζει γλιστράει και υποχωρεί 2 μέτρα. Σε πόσες ημέρες θα φτάσει τελικά στην κορυφή του τοίχου;

Λύση

Ένα τούβλο ζυγίζει ένα κιλό και μισό τούβλο. Πόσα κιλά ζυγίζουν τα δύο τούβλα;

Λύση

Πόσο είναι το 1/2 των 2/3 των 3/4 των 4/5 των 5/6 των 6/7 των 7/8 των 8/9 των 9/10 του χίλια;

Λύση

Ένα αντρόγυνο γύριζε από ψώνια στο Σούπερ Μάρκετ φορτωμένοι με τσάντες. Ο άντρας άρχισε να διαμαρτύρεται στην γυναίκα του ότι οι τσάντες που κουβαλάει είναι πολύ βαριές. "Τι διαμαρτύρεσαι;" του λέει εκείνη. "Αν μου έδινες μία από τις τσάντες σου, θα είχα τις διπλάσιες απ' ότι εσύ, ενώ αν σου έδινα εγώ μία δικιά μου, θα είχαμε τις ίδιες". Πόσες τσάντες κρατούσε ο καθένας;

Λύση

Ένας κλέφτης μπαίνει σε ένα χωράφι και κλέβει ένα πανέρι με πορτοκάλια. Στον δρόμο τον βλέπει ένας χωρικός και του λέει πως για να μην τον καρφώσει θα πρέπει να του δώσει τα μισά από τα πορτοκάλια που έχει στο πανέρι του και μισό πορτοκάλι ακόμα. Ο κλέφτης συμβιβάζεται και φεύγει. Παρακάτω τον σταματάει κι άλλος χωρικός και του λέει το ίδιο πράγμα: θέλει τα μισά από τα πορτοκάλια που του έχουν απομείνει και μισό πορτοκάλι ακόμα. Ο κλέφτης τα δίνει και αυτά, αλλά παρακάτω πέφτει και σε τρίτο χωρικό ο οποίος του λέει πάλι το ίδιο. Όταν ο κλέφτης δίνει και σ' αυτόν τα πορτοκάλια που του ζητούσε, κοιτάζει μέσα στο πανέρι και βλέπει πως του έχει απομείνει μόνο ένα πορτοκάλι. Πόσα είχε κλέψει αρχικά;

Λύση

Ένας ηλικιωμένος Αραβας είπε στους τρεις γιους του ότι τους αφήνει κληρονομιά τις καμήλες του. Ο μεγαλύτερος γιος θα έπαιρνε τις μισές καμήλες, ο μεσαίος το 1/3 και ο μικρότερος το 1/9 των καμηλών του. Αφού πέθανε ο πατέρας τους, πήγαν να δουν τις καμήλες αλλά διαπίστωσαν πως ήταν 17 και δεν μπορούσαν να τις μοιράσουν όπως τους είχε πει. Δεν ήθελαν να πουλήσουν ούτε ν' αγοράσουν καμία. Εκείνη τη στιγμή εμφανίστηκε καβάλα στην καμήλα του ο Αμπντουλάχ, ο οποίος βρήκε τρόπο να μοιράσουν τις καμήλες όπως ήθελε ο πατέρας τους. Τι τους είπε να κάνουν;

Λύση

Πέντε σκύλοι πιάνουν πέντε γάτες σε πέντε λεπτά. Πόσοι σκύλοι πιάνουν 100 γάτες σε 100 λεπτά;

Λύση