 Τέσσερις φίλες (***)
Τέσσερις φίλες (***)
 Τέσσερις φίλες (***)
Τέσσερις φίλες (***)
Τέσσερις φίλες, η Άννα, η Βάσω, η Γωγώ και η Δανάη βρίσκονται σε ένα δωμάτιο όπου συμβαίνουν τα εξής γεγονότα:
γ1. Όλες κοιτάζουν κάποια (όχι απαραίτητα την ίδια και όχι απαραίτητα μόνο μία).
γ2. Όποιες κοιτάζει η Άννα, τις κοιτάζει και η Βάσω.
γ3. Η Βάσω δεν κοιτάζει τη Δανάη.
γ4. Καμία δεν κοιτάζει τον εαυτό της.
Με βάση τα πιο πάνω δεδομένα, χαρακτηρίστε ως αληθή, ψευδή ή μη αποφασίσιμη καθεμία από τις πιο κάτω προτάσεις:
π1. Η Βάσω κοιτάζει τη Γωγώ.
π2. Η Βάσω κοιτάζει την Άννα.
Χημικοί και αλχημιστές (**)
Σε ένα συνέδριο συμμετείχαν 100 άνθρωποι οι οποίοι ήταν είτε χημικοί είτε αλχημιστές. Ρωτήθηκαν οι 50 από αυτούς αν στους υπόλοιπους που συμμετέχουν στο συνέδριο (χωρίς δηλαδή να υπολογίζουν τον εαυτό τους) υπάρχουν περισσότεροι χημικοί ή αλχημιστές και όλοι απάντησαν πως οι αλχημιστές ήταν περισσότεροι. Γνωρίζουμε πως οι χημικοί λένε πάντοτε την αλήθεια, ενώ οι αλχημιστές λένε πάντοτε ψέματα. Πόσοι χημικοί και πόσοι αλχημιστές συμμετείχαν στο συνέδριο;
Γνωριμίες (*****)
Σε μια πόλη οποιοιδήποτε δύο γνωστοί δεν έχουν κοινούς γνωστούς και οποιοιδήποτε δύο άγνωστοι έχουν ακριβώς δύο κοινούς γνωστούς.
Αποδείξτε ότι όλοι οι κάτοικοι έχουν τον ίδιο αριθμό γνωστών.
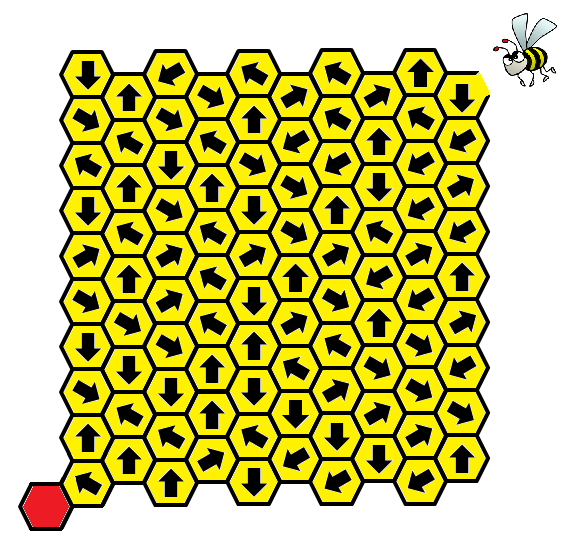
Η πεισματάρα μέλισσα (****)
Μια μέλισσα εισέρχεται σε μια κερήθρα - λαβύρινθο και προσπαθεί να φτάσει στο κόκκινο κελί όπου βρίσκεται αποθηκευμένος ο βασιλικός πολτός. Από το κάθε κελί μπορεί να κινηθεί μόνο προς το κελί που δείχνει το βέλος και σε κάθε της κίνηση, το βέλος του κελιού που βρισκόταν πριν, περιστρέφεται κατά 60 μοίρες δεξιόστροφα. Αν βρεθεί σε ακριανό κελί που το βέλος του δείχνει εκτός της κερήθρας, τότε αυτό το βέλος περιστρέφεται δεξιόστροφα μέχρι να δείξει κάποιο άλλο κελί. Αν βρεθεί ξανά στο σημείο απ' όπου μπήκε τότε απλά ξαναμπαίνει στον λαβύρινθο. Υποθέτουμε πως η μέλισσα έχει απεριόριστο πείσμα και χρόνο και στη διάθεσή της.
Μπορείτε να αποδείξετε πως στο τέλος θα καταλήγει πάντοτε στο κόκκινο κελί και μάλιστα με οποιαδήποτε αρχική διάταξη των βελών;
Αστρονόμοι (***)
Στον γαλαξία Sombrero υπάρχουν Ν πλανήτες που φιλοξενούν νοήμονα ζωή. Κάθε πλανήτης έχει πάνω του έναν αστρονόμο που παρατηρεί τον πλησιέστερο σε αυτόν πλανήτη. Όλες οι αποστάσεις μεταξύ των πλανητών είναι διαφορετικές. Να αποδειχτεί πως αν το Ν είναι περιττό τότε υπάρχει κάποιος πλανήτης που δεν τον παρατηρεί κανένας αστρονόμος.
Δύο ψεύτρες (**)
Η Αμαλία και η Βασιλική λένε πάντοτε ψέματα. Μια μέρα είχαν τον παρακάτω διάλογο σχετικά με τις ηλικίες τους:
Αμαλία: Δεν είμαι πάνω από 30.
Βασιλική: Εγώ είμαι μόνο 28.
Αμαλία: Ας γελάσω! Εσύ είσαι τουλάχιστον 29.
Βασιλική: Μιλάς κι εσύ που είσαι τουλάχιστον 5 χρόνια μεγαλύτερή μου.
Πόσων χρονών είναι η καθεμία τους;
Αντιστοίχιση κλειδιών (***)
Ένα καινούργιο ξενοδοχείο διαθέτει 10 δωμάτια. Ο ξενοδόχος μπέρδεψε τα 10 κλειδιά τους πριν προλάβει να τους περάσει τους αριθμούς των δωματίων και έτσι τώρα δεν έχει κανένα τρόπο να τα αντιστοιχίσει στις πόρτες που ανοίγουν, παρά μόνο δοκιμάζοντάς τα πάνω τους.
Ποιος είναι ο μέγιστος αριθμός δοκιμών που μπορεί να χρειαστούν προκειμένου να αντιστοιχίσει το κάθε κλειδί στη σωστή πόρτα;
Χρυσό, ασημένιο, χάλκινο (***)
Κάποιος βάζει ένα χρυσό, ένα ασημένιο και ένα χάλκινο νόμισμα πάνω σε ένα τραπέζι και σας λέει πως αν κάνετε μια αληθή δήλωση θα σας δώσει ένα από τα τρία νομίσματα, όποιο θέλει αυτός, ενώ αν κάνετε μια ψευδή δήλωση δεν θα σας δώσει τίποτα. Με ποια δήλωση θα καταφέρετε να πάρετε το χρυσό νόμισμα;
Ραντεβού στα τυφλά (***)
Ο Άρης θέλει να επισκεφτεί την παλιά του φίλη Βίκυ που μένει στον κεντρικό δρόμο ενός χωριού. Ο δρόμος έχει 50 σπίτια, μοιρασμένα σε δυο οικισμούς και αριθμημένα από 1-20 στον 1ο και από 21-50 στο 2ο οικισμό. Ο Άρης έχει ξεχάσει τον αριθμό του σπιτιού της Βίκυς και ρωτάει σχετικά έναν περαστικό. Ο περαστικός δεν του απαντά ευθέως, αλλά του λέει σε ποιον ακριβώς οικισμό βρίσκεται το σπίτι, αν ο αριθμός του είναι μονός ή ζυγός και αν είναι ή όχι τέλειο τετράγωνο. Ο Άρης τότε, για να σιγουρευτεί απόλυτα, ρωτάει τον περαστικό αν ο αριθμός του σπιτιού περιέχει το ψηφίο 4. Παίρνοντας την απάντηση, ο Άρης σιγουρεύεται και πηγαίνει στο σπίτι που συμπέρανε ότι έμενε η Βίκυ.
Χτυπάει το κουδούνι, αλλά αντί της Βίκυς του ανοίγει ένας άντρας που του συστήθηκε ως Γιάννης. Ο Γιάννης εξήγησε γελώντας στον Άρη πως ο περαστικός που του είχε δώσει τις πληροφορίες ήταν ο μεγαλύτερος ψεύτης του χωριού και δεν έλεγε ποτέ την αλήθεια. Τότε ο Άρης σκέφτηκε για μια στιγμή και είπε: Ευχαριστώ, τώρα ξέρω τον πραγματικό αριθμό του σπιτιού της Βίκυς!
Ποιος ήταν ο αριθμός του σπιτιού της Βίκυς και ποιος του Γιάννη;
Οικογενειακό σκάκι (**)
Μια οικογένεια διοργάνωσε ένα τουρνουά σκάκι. Οι παίκτες ήταν η μητέρα, ο αδελφός της, η κόρη της και ο γιος της. Δύο από τα μέλη της οικογένειας ήταν δίδυμοι. Ο νικητής του τουρνουά είχε την ίδια ηλικία με τον τελευταίο της κατάταξης και αντίθετο φύλο από τον δίδυμο του τελευταίου. Ποιος κέρδισε το τουρνουά και ποιος ήρθε τελευταίος;
Το στέμμα του βασιλιά (***)
Τα παλιά τα χρόνια δικαζόταν ένας άνθρωπος με τη βαρύτατη κατηγορία ότι είχε κλέψει το στέμμα του βασιλιά. Ήταν γνωστό πως ο κατηγορούμενος ανήκε είτε στη φυλή των Ιώνων είτε στη φυλή των Χετταίων. Ήταν επίσης γνωστό ότι όλοι οι Ίωνες έλεγαν πάντοτε την αλήθεια και όλοι οι Χετταίοι έλεγαν πάντοτε ψέματα.
Ζήτησε λοιπόν ο δικαστής από τον κατηγορούμενο να πει κάτι, μήπως και καταλάβαινε αν ήταν αυτός ο ένοχος. Ο κατηγορούμενος έκανε μια δήλωση και αμέσως ο δικαστής τον αθώωσε.
Όταν ρώτησαν τον δικαστή αν ο κατηγορούμενος είχε πει την αλήθεια, εκείνος απάντησε: «δεν έχω ιδέα!».
Βρείτε μια δήλωση που θα μπορούσε να είχε κάνει ο κατηγορούμενος.
Οι Έλληνες είναι φίλοι μας (**)
Αποδείξτε πως είναι βέβαιο ότι υπάρχουν τουλάχιστον δύο Έλληνες με τον ίδιο αριθμό Ελλήνων φίλων.
Διευκρίνιση: Οι σχέσεις φιλίας θεωρούνται αμοιβαίες.
Καραφλοχώρι (**)
Στο Καραφλοχώρι κάθε 10 χρόνια γίνεται απογραφή στις τρίχες του πληθυσμού. Η τελευταία απογραφή κατέληξε στα εξής συμπεράσματα:
1. Δεν υπήρχαν δύο κάτοικοι με τον ίδιο αριθμό τριχών στο κεφάλι τους.
2. Κανένας κάτοικος δεν είχε ακριβώς 317 τρίχες στο κεφάλι του.
3. Υπήρχαν περισσότεροι κάτοικοι από τις τρίχες στο κεφάλι οποιουδήποτε κατοίκου.
Ποιος είναι ο μέγιστος αριθμός κατοίκων που μπορεί να έχει το Καραφλοχώρι;
Πόσοι πήραν μπαλόνι; (**)
Σε μια γιορτή του σχολείου, η δασκάλα ζήτησε από 10 παιδιά να παίξουν ένα παιχνίδι. Τους είπε να κλείσουν τα μάτια και φόρεσε στον καθένα τους είτε ένα κόκκινο είτε ένα άσπρο καπέλο. Μετά τους είπε να ανοίξουν τα μάτια τους και να δουν τα καπέλα που φοράνε τα υπόλοιπα παιδιά.
Όποιο παιδάκι έβλεπε τέσσερα ή περισσότερα κόκκινα καπέλα θα έπαιρνε δώρο ένα μπαλόνι. Στο τέλος του παιχνιδιού ένα παιδάκι ζήλεψε που κάποιο άλλο πήρε μπαλόνι ενώ αυτό όχι. Πόσα πήραν μπαλόνι;
Χώρισμα της τράπουλας (****)
Βρίσκεστε σε ένα σκοτεινό δωμάτιο με τα μάτια σας δεμένα και κάποιος σας δίνει μια κανονική τράπουλα με 52 φύλλα. Σας λέει πως στην τράπουλα αυτή υπάρχουν σε τυχαίες θέσεις 13 φύλλα τα οποία είναι γυρισμένα ανάποδα, δηλαδή είναι ανοιχτά ενώ τα υπόλοιπα είναι κλειστά. Δεν υπάρχει κανένας τρόπος να ξεχωρίσετε τα ανοιχτά από τα κλειστά, ούτε να εντοπίσετε τις θέσεις τους.
Το ζητούμενο είναι να χωρίσετε τα 52 φύλλα σε δύο στοίβες (όχι απαραίτητα με τον ίδιο συνολικό αριθμό φύλλων η κάθε μία) έτσι ώστε η κάθε στοίβα να έχει τον ίδιο αριθμό ανοιχτών φύλλων.
Χειραψίες (****)
Πέντε ζευγάρια συναντιόνται για φαγητό σε ένα εστιατόριο. Πριν καθίσουν να φάνε γίνονται οι απαραίτητες συστάσεις γιατί κάποιοι δεν γνωρίζονταν μεταξύ τους. Όσοι δεν γνωρίζονταν ανταλλάσσουν μια χειραψία. Φυσικά τα αντρόγυνα δεν ανταλλάσσουν χειραψία γιατί γνωρίζονται μεταξύ τους.
Στο τέλος της διαδικασίας χειραψιών, ο Γιάννης ρωτάει τον καθένα τους πόσες χειραψίες έκανε και παίρνει τις απαντήσεις 0, 1, 2, 3, 4, 5, 6, 7 και 8, αλλά δεν ξέρουμε ποιος απάντησε τι.
Πόσες χειραψίες αντάλλαξε η γυναίκα του Γιάννη;
Πραγματικό μέντιουμ (***)
Επιτέλους, μετά από χρόνια ερευνών, βρέθηκε ένα μέντιουμ που προέβλεπε σωστά το μέλλον με ποσοστό επιτυχίας 100%. Δεχόταν έναν πελάτη στο σπίτι του, αυτός του έκανε μια ερώτηση για το μέλλον και το μέντιουμ απαντούσε μόνο με ναι ή όχι. Απαραίτητη προϋπόθεση για να λειτουργήσει σωστά η πρόβλεψη ήταν ο πελάτης να μην μπορεί να επηρεάσει το μέλλον ανάλογα με την απάντηση του μέντιουμ. Παρόλα αυτά ένας πελάτης κατάφερε να του κάνει μια ερώτηση όπου το μέντιουμ προέβλεψε το μέλλον λανθασμένα. Τι το ρώτησε;
Οι τρεις Σοφοί (******)
Σ' αυτό το πρόβλημα δεν έχουν μπει κατά λάθος 6 αστεράκια. Σύμφωνα πάλι με την άποψη του George Boolos, πρόκειται για τον δυσκολότερο γρίφο λογικής που διατυπώθηκε ποτέ. Μια αρχική του εκδοχή παρουσιάστηκε από τον Raymond Smullyan στο βιβλίο του "What is the Name of This Book". Η εκδοχή που παρουσιάζεται εδώ έχει προκύψει μετά από αρκετές παραλλαγές και βελτιώσεις έως και το 2008.
Κάποιος επισκέπτης ενός νησιού βρέθηκε σε ένα λόφο μπροστά σε τρεις Σοφούς. Ο ένας Σοφός λέγεται Ειλικρινής και λέει πάντα την αλήθεια. Ο άλλος λέγεται Ψεύτης και λέει πάντοτε ψέματα. Ο τρίτος λέγεται Τυχαίος και απαντάει στην τύχη, πότε αλήθεια και πότε ψέματα.
Ο επισκέπτης δεν ξέρει ποιος Σοφός έχει ποια ιδιότητα, γι αυτό τους συμβολίζει με τα γράμματα Α, Β και Γ. Οι Σοφοί του βάζουν την πρόκληση να ανακαλύψει την ιδιότητα του καθενός, κάνοντάς τους μόνο τρεις ερωτήσεις οι οποίες θα πρέπει να απαντηθούν όλες με ναι ή όχι. Μια επιπλέον δυσκολία που του παρουσιάστηκε είναι πως οι Σοφοί, παρόλο που γνωρίζουν τέλεια τη γλώσσα του επισκέπτη, απαντούν μόνο στη δική τους γλώσσα με τις λέξεις da ή ja. Η μία από αυτές σημαίνει ναι και η άλλη όχι, χωρίς όμως να ξέρει ο επισκέπτης ποια είναι ποια.
Δίνονται οι πιο κάτω διευκρινίσεις:
1) Ο κάθε Σοφός γνωρίζει την ιδιότητα των άλλων δύο.
2) Η κάθε ερώτηση απαντιέται από έναν μόνο Σοφό. Δεν είναι απαραίτητο να γίνει μία ερώτηση σε κάθε Σοφό. Μπορεί ένας από αυτούς να ερωτηθεί περισσότερες από μία φορές.
3) Το ποια θα είναι η δεύτερη ή η τρίτη ερώτηση μπορεί να εξαρτάται από τις απαντήσεις των προηγούμενων ερωτήσεων.
4) Οι απαντήσεις da ή ja του Τυχαίου είναι εντελώς τυχαίες και δεν εξαρτώνται από την ερώτηση. Συνεπώς δεν μπορεί να εξαχθεί οποιαδήποτε χρήσιμη πληροφορία από τις απαντήσεις αυτές.
5) Και οι τρεις ερωτήσεις πρέπει να απαντηθούν αποκλειστικά με da ή ja. Αν κάποια ερώτηση φέρει έναν Σοφό μπροστά σε αντίφαση, τότε ο επισκέπτης χάνει την πρόκληση.
Πώς μπορεί να προσδιοριστεί η ταυτότητα του κάθε Σοφού με τρεις μόνο ερωτήσεις;
Επειδή ο γρίφος είναι δύσκολος, ξεκινώ τη λύση του όχι με τις ερωτήσεις που πρέπει να γίνουν, αλλά με μια σειρά υποδείξεων που βοηθούν στην επίλυσή του. Όσες λιγότερες υποδείξεις διαβάσετε, που δεν τις είχατε σκεφτεί από μόνοι σας, τόσο πιο περήφανοι θα πρέπει να αισθάνεστε αν φτάσετε στη λύση.
Πεντάρι στο ΠΡΟ-ΠΟ (**)
Ποιος είναι ο ελάχιστος αριθμός στηλών που πρέπει να παίξει κανείς στο ΠΡΟ-ΠΟ (το κλασσικό με τους 13 αγώνες) για να πιάσει οπωσδήποτε πεντάρι;
Ποιος είναι ο κατάσκοπος; (*****)
Σύμφωνα με την άποψη του George Boolos, καθηγητή φιλοσοφίας και μαθηματικής λογικής στο MIT, πρόκειται για τον πιο ευφυή γρίφο λογικής που διατυπώθηκε ποτέ. Προκαλώ τον αναγνώστη να προσπαθήσει να τον λύσει, αφού καταλάβει τη λογική των μεταγρίφων, λύνοντας πρώτα τα "Δύο φίλοι" και "Οι δύο δίδυμοι" στην κατηγορία της Λογικής και την "Περίπλοκη απογραφή" στην κατηγορία των Συνδυασμών.
Η υπόθεση αφορά στη δίκη τριών προσώπων, των Α, Β και Γ. Ο ένας από τους τρεις ήταν ιππότης, συνεπώς έλεγε πάντοτε την αλήθεια, ο άλλος ήταν ιπποκόμος, δηλαδή έλεγε πάντοτε ψέματα και ο τρίτος ήταν κατάσκοπος και έλεγε πότε αλήθεια και πότε ψέματα. Η δίκη γινόταν για να εντοπιστεί και να καταδικαστεί ο κατάσκοπος. Φυσικά, ο δικαστής δεν ήξερε ποιος είναι ποιος.
Αρχικά ζητήθηκε από τον Α να κάνει μια δήλωση. Εκείνος δήλωσε είτε ότι ο Γ ήταν ιπποκόμος, είτε ότι ο Γ ήταν ο κατάσκοπος - εμείς όμως δεν γνωρίζουμε ποια ήταν η δήλωσή του, παρά μόνο ο δικαστής. Στη συνέχεια ο Β δήλωσε είτε ότι ο Α ήταν ιππότης, είτε ότι ο Α ήταν ιπποκόμος, είτε ότι ο Α ήταν ο κατάσκοπος. Τέλος, ο Γ δήλωσε είτε ότι ο Β ήταν ιππότης, είτε ότι ο Β ήταν ιπποκόμος, είτε ότι ο Β ήταν ο κατάσκοπος. Με βάση τα παραπάνω, ο δικαστής κατάφερε να προσδιορίσει ποιος ήταν ο κατάσκοπος και τον καταδίκασε.
Την υπόθεση αυτή τη διηγήθηκαν σε έναν λογικολόγο, ο οποίος αφού μελέτησε το πρόβλημα, αποφάνθηκε ότι δεν είχε επαρκείς πληροφορίες για να εντοπίσει τον κατάσκοπο. Τότε ανέφεραν στον λογικολόγο την ακριβή δήλωση του Α για τον Γ και μόνο έτσι μπόρεσε να προσδιορίσει ποιος ήταν ο κατάσκοπος. Ποιος ήταν, αλήθεια; Ο Α, ο Β ή ο Γ;
Δύο φίλοι (**)
Κάποτε βρέθηκα μπροστά σε δύο φίλους που ήξερα ότι ο ένας λέει πάντοτε την αλήθεια και ο άλλος πότε αλήθεια και πότε ψέματα, αλλά δεν ήξερα ποιος είναι ποιος. Ρώτησα λοιπόν τον πρώτο εάν ο φίλος του λέει πάντα αλήθεια και εκείνος μου απάντησε με "ναι" ή "όχι". Αμέσως τότε κατάλαβα ποιος έλεγε πάντα αλήθεια και ποιος πότε αλήθεια και πότε ψέματα. Τι λέει ο καθένας;
Δρομολόγια τρένων (**)
Η Αννα μένει κοντά σ' έναν σταθμό του τρένου και το χρησιμοποιεί για να πηγαίνει να βλέπει τον φίλο της. Αυτό που την προβληματίζει όμως είναι το εξής: Οποιαδήποτε ώρα και αν πάει στον σταθμό, το τρένο που πάει προς την αντίθετη κατεύθυνση έρχεται σχεδόν πάντα πριν από αυτό που πάει προς το σπίτι του φίλου της. Γιατί συμβαίνει αυτό;
Σημείωση: Και τα δύο δρομολόγια περνούν κάθε δέκα λεπτά και μάλιστα ακριβώς την ίδια ώρα κάθε ημέρα.
Δήλωση ειλικρίνειας (*)
Ο Νίκος κάνει την εξής δήλωση: "Όπως όλος ο κόσμος έτσι και 'γω, λέω πάντοτε ψέματα". Τι μπορούμε να συμπεράνουμε από τη δήλωσή του; Λέει πάντα αλήθεια, πάντοτε ψέματα ή πότε αλήθεια και πότε ψέματα; Επίσης η δήλωσή του είναι αληθής ή ψευδής;
Την κυρία ή την τίγρη; (**)
Ένας βασιλιάς έβαλε έναν κρατούμενο μπροστά από δύο πόρτες. Η πόρτα Νο 1 έγραφε: "Σ' ΑΥΤΟ ΤΟ ΔΩΜΑΤΙΟ ΥΠΑΡΧΕΙ ΜΙΑ ΚΥΡΙΑ ΚΑΙ ΣΤΟ ΔΙΠΛΑΝΟ ΜΙΑ ΤΙΓΡΗ". Η πόρτα Νο 2 έγραφε: "ΣΤΟ ΕΝΑ ΑΠΟ ΤΑ ΔΥΟ ΔΩΜΑΤΙΑ ΥΠΑΡΧΕΙ ΜΙΑ ΚΥΡΙΑ ΚΑΙ ΣΤΟ ΑΛΛΟ ΜΙΑ ΤΙΓΡΗ". Ο βασιλιάς είπε στον κρατούμενο ότι η μία από τις δύο επιγραφές γράφει την αλήθεια και η άλλη ψέματα. Εάν ο κρατούμενος ανοίξει την πόρτα με την κυρία θα την παντρευτεί ενώ αν ανοίξει την πόρτα με την τίγρη θα φαγωθεί. Ποια πόρτα πρέπει να ανοίξει ο κρατούμενος;
Παράξενος δεκαψήφιος (***)

Στις 10 θέσεις του παραπάνω σχήματος γράψτε έναν δεκαψήφιο αριθμό, ώστε το ψηφίο στην πρώτη θέση να δείχνει τον συνολικό αριθμό των μηδενικών του αριθμού, το ψηφίο στη θέση με την ένδειξη 1 να δείχνει τον συνολικό αριθμό των 1 και ούτω καθεξής, μέχρι την τελευταία θέση, το ψηφίο της οποίας πρέπει να δείχνει τον συνολικό αριθμό των 9 στον αριθμό. Η λύση είναι μοναδική.
Οι καμήλες του Αμπντουλάχ (**)
"Ο Αμπντουλάχ είναι πολύ πλούσιος", είπε ο Αλή Μπαμπά. "Συγκεκριμένα έχει τουλάχιστον 100 καμήλες". "Αποκλείεται", είπε ο Ισμαήλ. "Είμαι σίγουρος ότι έχει λιγότερες από 100". "Απ' όσο ξέρω εγώ, έχει τουλάχιστον μία καμήλα", πρόσθεσε ο Φαρούχ. Αν μόνο ένας από τους τρεις έχει δίκιο, τότε πόσες καμήλες έχει ο Αμπντουλάχ;
Οι δέκα προτάσεις (*)
Έχουμε τις παρακάτω δέκα προτάσεις. Ποιες από αυτές είναι αληθείς και ποιες ψευδείς;
1) Μία μόνο από αυτές τις προτάσεις είναι ψευδής.
2) Δύο μόνο από αυτές τις προτάσεις είναι ψευδείς.
3) Τρεις μόνο από αυτές τις προτάσεις είναι ψευδείς.
4) Τέσσερις μόνο από αυτές τις προτάσεις είναι ψευδείς.
5) Πέντε μόνο από αυτές τις προτάσεις είναι ψευδείς.
6) Έξι μόνο από αυτές τις προτάσεις είναι ψευδείς.
7) Επτά μόνο από αυτές τις προτάσεις είναι ψευδείς.
8) Οκτώ μόνο από αυτές τις προτάσεις είναι ψευδείς.
9) Εννέα μόνο από αυτές τις προτάσεις είναι ψευδείς.
10) Δέκα από αυτές τις προτάσεις είναι ψευδείς.
Κόκκινο - πράσινο - μπλε (**)
Τρεις φίλοι, ο κύριος Κόκκινος, ο κύριος Μπλε και ο κύριος Πράσινος, κάθονται και συζητούν. Ο ένας φοράει κόκκινο, ο άλλος μπλε και ο τρίτος πράσινο κοστούμι. Τον λόγο παίρνει αυτός που φοράει το μπλε κοστούμι και λέει: "Προσέξατε κάτι; Κανένας μας δεν φοράει κοστούμι ίδιο με τ' όνομά του". "Πράγματι, έχεις δίκιο. Δεν το 'χα προσέξει", συμπληρώνει ο κύριος Κόκκινος. Τι χρώμα κοστούμι φοράει ο καθένας;
Πανέρια με φρούτα (***)
Έχουμε τρία κλειστά πανέρια και μία επιγραφή κρεμασμένη πάνω στο καθένα. Η πρώτη γράφει "ΠΟΡΤΟΚΑΛΙΑ", η δεύτερη γράφει "ΜΑΝΤΑΡΙΝΙΑ" και η τρίτη γράφει "ΠΟΡΤΟΚΑΛΙΑ ΚΑΙ ΜΑΝΤΑΡΙΝΙΑ". Ξέρουμε ότι και οι τρεις επιγραφές είναι τοποθετημένες λάθος. Πώς μπορούμε βγάζοντας ένα φρούτο από ένα μόνο πανέρι και χωρίς να κοιτάξουμε μέσα ή να ψαχουλέψουμε, να βάλουμε τις επιγραφές στη σωστή τους θέση;
Οι δύο δίδυμοι (***)
Δύο δίδυμοι παρουσιάζονται στο δικαστήριο. Ο ένας από αυτούς λέει πάντοτε ψέματα, ενώ ο άλλος πότε ψέματα και πότε την αλήθεια. Ο ένας δίδυμος, ο Τζων, είχε διαπράξει ένα έγκλημα. (Ο Τζων δεν ήταν κατ' ανάγκη αυτός που έλεγε πάντοτε ψέματα). "Είσαι ο Τζων;" ρωτάει ο δικαστής τον πρώτο δίδυμο. "Ναι, είμαι" του απαντάει. "Είσαι ο Τζων;" ξαναρωτάει ο δικαστής τον δεύτερο δίδυμο. Εκείνος του απάντησε ή "ναι" ή "όχι" και αμέσως ο δικαστής βρήκε ποιος ήταν ο Τζων. Ήταν ο πρώτος ή ο δεύτερος δίδυμος;
Ψεύτες ανθρωποφάγοι (**)
Ένας εξερευνητής έχει βρεθεί σε μία ζούγκλα που κατοικείται από δύο φυλές ιθαγενών. Η πρώτη φυλή αποτελείται από φιλήσυχους ιθαγενείς οι οποίοι λένε πάντα την αλήθεια. Η δεύτερη φυλή αποτελείται από ανθρωποφάγους που λένε πάντοτε ψέματα. Κατά τα άλλα είναι απολύτως όμοιοι. Τρέχοντας για να ξεφύγει από ένα λιοντάρι που τον κυνηγούσε, βρέθηκε μπροστά σε ένα σταυροδρόμι του οποίου, όπως γνώριζε, ο ένας δρόμος οδηγούσε στο χωριό των φιλήσυχων και ο άλλος στο χωριό των ανθρωποφάγων. Δεν μπορούσε όμως να θυμηθεί ποιος δρόμος οδηγεί πού. Μπροστά στο σταυροδρόμι καθόταν ένας ιθαγενής μιας εκ των δύο φυλών. Ο εξερευνητής είχε χρόνο να του κάνει μόνο μία ερώτηση. Τι θα τον ρωτήσει για να οδηγηθεί στο χωριό των φιλήσυχων ιθαγενών;
Εδώ είναι ο παράδεισος (****)
Ένας άνθρωπος, αμέσως μόλις πεθαίνει, βρίσκεται μπροστά από δύο πόρτες που φυλάσσονται από δύο φρουρούς. Η μία πόρτα οδηγεί στον παράδεισο και η άλλη στην κόλαση. Ο ένας από τους δύο φρουρούς λέει πάντα την αλήθεια και ο άλλος πάντοτε ψέματα και αυτό το γνωρίζουν και οι τρεις τους, δεν ξέρουμε όμως ποιος φρουρός στέκεται μπροστά από ποια πόρτα. Πώς με μία μόνο ερώτηση σε έναν από τους δύο φρουρούς, θα βρει την πόρτα που οδηγεί στον παράδεισο;
Το συρτάρι με τα γάντια (*)
Ένας σκιέρ ξυπνάει τα χαράματα και ετοιμάζεται να πάει για σκι. Σ' ένα συρτάρι έχει 4 μαύρα και 8 μπλε μάλλινα γάντια. Δυστυχώς το δωμάτιο είναι πολύ σκοτεινό για να διακρίνει τα χρώματά τους. Πόσα γάντια πρέπει να πάρει τουλάχιστον μαζί του για να είναι σίγουρος ότι έχει δύο του ίδιου χρώματος, χωρίς ν' ανάψει το φως και ξυπνήσει τη γυναίκα του;
Ανακάτεμα φλιτζανιών (***)
Έχουμε δύο ίδια γεμάτα φλιτζάνια. Το ένα περιέχει τσάι και το άλλο καφέ. Παίρνουμε μία κουταλιά τσάι, την ρίχνουμε στον καφέ και ανακατεύουμε. Μετά παίρνουμε μία κουταλιά από το μείγμα και την ρίχνουμε στο τσάι. Το φλιτζάνι με το τσάι θα περιέχει περισσότερο καφέ ή το φλιτζάνι με τον καφέ περισσότερο τσάι;
Ένα μπουκέτο με λουλούδια (**)
Έχω ένα μπουκέτο με λουλούδια. Όλα τα λουλούδια είναι τριαντάφυλλα εκτός από δύο, όλα είναι γαρίφαλα εκτός από δύο και όλα είναι μαργαρίτες εκτός από δύο. Πόσα λουλούδια απ' το κάθε είδος έχει το μπουκέτο;