Γρίφοι Ανάλυσης

Φανέλες και σορτς (****)

Σε μία ομάδα με 33 αθλητές, τέθηκαν σε όλους με τη σειρά οι παρακάτω δύο ερωτήσεις: «πόσοι άλλοι αθλητές φοράνε ίδιο μέγεθος φανέλας με εσένα» και «πόσοι άλλοι αθλητές φοράνε ίδιο μέγεθος σορτς με εσένα». Στις 66 απαντήσεις που δόθηκαν, υπήρχαν όλοι οι αριθμοί από 0 έως 10 (ανεξαρτήτως από φανέλες ή σορτς). Δείξτε ότι υπάρχουν δύο αθλητές που φοράνε ίδιο μέγεθος φανέλας και ίδιο μέγεθος σορτς.

Λύση

Ένα αόρατο εχθρικό υποβρύχιο ξεκινάει σε χρόνο t=0 sec από ένα λιμάνι και κινείται βυθισμένο σε ευθεία γραμμή προς γνωστή κατεύθυνση, με μια άγνωστη αλλά σταθερή και ακέραια σε μέτρο ταχύτητα (σε m/sec). Εσείς διαθέτετε ένα σύστημα εκτόξευσης τοποθετημένο πάνω στο λιμάνι και επαρκή αριθμό βλημάτων, με δυνατότητα ρίψης ενός βλήματος ανά δευτερόλεπτο, από χρόνο t=1 sec και μετά, τα οποία πέφτουν με ακρίβεια σε οποιοδήποτε σημείο της θάλασσας θέλετε κάθε φορά. Με ποια στρατηγική θα βυθίσετε στα σίγουρα το υποβρύχιο;
Διευκρινίσεις: 1) Θεωρήστε αμελητέο τον χρόνο από την πυροδότηση μέχρι την άφιξη κάθε βλήματος στο στόχο. 2) Θεωρήστε πως έχετε απεριόριστο χώρο και χρόνο στη διάθεσή σας.

Λύση

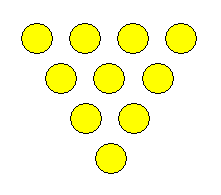
Τα 10 νομίσματα της εικόνας σχηματίζουν ένα τρίγωνο όπου η μία του κορυφή βρίσκεται προς τα κάτω. Μπορείτε μετακινώντας 3 νομίσματα να το αντιστρέψετε, δηλαδή να κάνετε τη μία του κορυφή να βρίσκεται πρς τα πάνω;

Λύση

15 μυρμήγκια περπατούν πάνω σε ένα ίσιο κλαδί μήκους 1 μέτρου με σταθερή ταχύτητα 10 εκατοστά το δευτερόλεπτο. Μπορούν να κινούνται είτε προς τα αριστερά είτε προς τα δεξιά. Κάθε φορά που συναντιόνται δύο μυρμήγκια αλλάζουν αμέσως και τα δύο κατευθύνσεις. Αν φτάσουν σε μία από τις δύο άκρες του κλαδιού πέφτουν. Ποιος είναι ο μέγιστος χρόνος που θα απαιτηθεί για να πέσουν όλα από το κλαδί; Μπορείτε να το αποδείξετε;

Λύση

"Εύχομαι το χτες να ήταν αύριο, ώστε σήμερα να ήταν Σάββατο". Ποια μέρα έκανα αυτή τη δήλωση;

Λύση

Μία κερματομηχανή δέχεται δύο είδη κερμάτων: μάρκα και φράγκα. Για κάθε κέρμα του ενός είδους που ρίχνουμε, μας επιστρέφει 3 κέρματα του άλλου είδους. Αν αρχικά έχουμε 5 μάρκα και 3 φράγκα, θα μπορούσαμε παίζοντας στην κερματομηχανή να αποκτήσουμε κάποια στιγμή ίσο αριθμό μάρκων και φράγκων; Αν ναι πώς, αν όχι γιατί;

Λύση

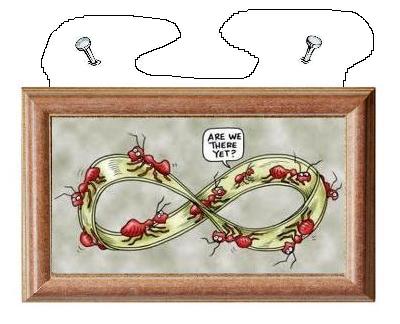
Μπορείτε να βρείτε πώς πρέπει να περάσει το σύρμα του πίνακα γύρω από τα δύο καρφιά έτσι ώστε όποιο καρφί και αν αφαιρεθεί από τον τοίχο, ο πίνακας να πέφτει κάτω;

Λύση

Χρησιμοποιώντας 26 μοναδιαίους κύβους φτιάχνουμε έναν μεγάλο κύβο 3x3x3, αφήνοντας κενή τη θέση ενός μοναδιαίου κύβου στο κέντρο του. Η κενή θέση μπορεί να καλύπτεται ολισθαίνοντας οποιονδήποτε γειτονικό της κύβο, οπότε μένει πλέον κενή η αρχική θέση του μετακινούμενου κύβου και αυτό μπορεί να επαναλαμβάνεται όσες φορές θέλουμε. Είναι εφικτό, με μια διαδοχή τέτοιων μετακινήσεων και οι 26 κύβοι να βρεθούν τελικά σε θέσεις συμμετρικές προς τις αρχικές τους θέσεις ως προς το κέντρο της διάταξης; Αν ναι με ποιον τρόπο, αν όχι γιατί;

Λύση

Σημείωση: Τα παρακάτω δύο προβλήματα, ακολουθούν τους ίδιους ακριβώς κανόνες με τον λυμένο γρίφο «Ευθείες από 9 νομίσματα» στην ίδια κατηγορία.

1ο πρόβλημα: Έχουμε 16 ίδια νομίσματα και πρέπει να τα τοποθετήσουμε έτσι ώστε να ακουμπάνε όλα πάνω σε ένα τραπέζι, χωρίς επικαλύψεις και να σχηματίζονται μεταξύ τους 15 ευθείες των 4 νομισμάτων η κάθε μία.

2ο πρόβλημα: Έχουμε 25 ίδια νομίσματα και πρέπει να τα τοποθετήσουμε έτσι ώστε να ακουμπάνε όλα πάνω σε ένα τραπέζι, χωρίς επικαλύψεις και να σχηματίζονται μεταξύ τους 18 ευθείες των 5 νομισμάτων η κάθε μία.

Λύση

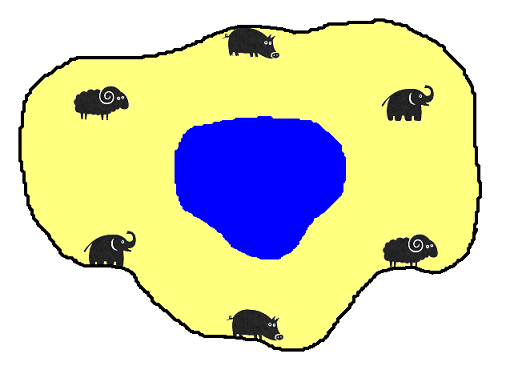
Ενώστε με τρεις γραμμές τα ζευγάρια των ίδιων ζώων, έτσι ώστε οι γραμμές σας να μην διασταυρώνονται και να μην περνούν μέσα από τη λίμνη ή έξω από τη ζούγκλα.

Λύση

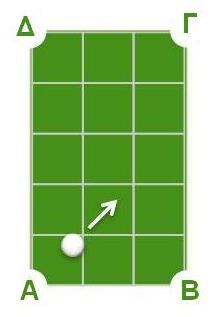
Αν στο μπιλιάρδο που φαίνεται στο σχήμα χτυπήσουμε την άσπρη μπάλα κατά γωνία 45° προς την κατεύθυνση του βέλους, σε ποια τρύπα θα μπει;

Λύση

Ποιος από τους δύο αριθμούς είναι μεγαλύτερος; Ο 17¹⁴ ή ο 31¹¹ ;
Βρείτε έναν τρόπο να το αποδείξετε με ελάχιστες πράξεις, χωρίς να χρησιμοποιήσετε κομπιουτεράκι ή λογαριθμικό πίνακα.

Λύση

Σε μια διαδήλωση έχουν κατέβει στην πλατεία πολλοί διαδηλωτές, όλοι τους οπλισμένοι με ένα γιαούρτι. Ξαφνικά τα αίματα ανάβουν και ο καθένας εκτοξεύει το γιαούρτι του προς τον πλησιέστερο σε αυτόν διαδηλωτή για να είναι σίγουρος πως θα τον πετύχει. Πόσα είναι τα περισσότερα γιαούρτια που μπορεί να φάει ο πιο άτυχος διαδηλωτής της συγκέντρωσης;
Διευκρινίσεις:
1) Όταν δύο διαδηλωτές απέχουν ακριβώς το ίδιο από αυτόν που ρίχνει το γιαούρτι, τότε το τρώει ο ένας από τους δύο στην τύχη.
2) Στη διαδήλωση δεν υπάρχουν πολιτικοί.

Δεύτερο ερώτημα:

Ας υποθέσουμε πως η διαδήλωση στο μέλλον γίνεται στο διάστημα. Έτσι οι διαδηλωτές είναι αστροναύτες που κινούνται ελεύθερα στο χώρο. Πόσα γιαούρτια μπορεί να φάει τώρα ο πιο άτυχος διαδηλωτής;

Σημείωση: Ο βαθμός δυσκολίας του γρίφου αναφέρεται στο πρώτο ερώτημα. Στο δεύτερο θα έβαζα 4 αστεράκια.

Λύση

Έχουμε οκτώ κομμάτια μιας αλυσίδας που αποτελούνται από επτά κρίκους το καθένα. Οι ακριανοί κρίκοι του κάθε τμήματος είναι κλειστοί. Θέλουμε να ενώσουμε και τα οκτώ τμήματα και να φτιάξουμε μια μεγάλη κυκλική αλυσίδα (οι άκρες της να ενώνονται).
Ένας τεχνίτης αναλαμβάνει να ανοίξει και να κλείσει όσους κρίκους του πούμε με κόστος 1 ευρώ ανά κρίκο (άνοιγμα - πέρασμα - κλείσιμο). Ποιο είναι το ελάχιστο κόστος που απαιτείται για να φτιάξουμε την αλυσίδα και ποιους κρίκους θα ζητήσουμε να μας ανοίξει;

Λύση

Τον περασμένο μήνα έκανα ένα ταξίδι με το αυτοκίνητό μου από την Αθήνα στη Θεσσαλονίκη. Επειδή ήμουν βιαστικός, ξεκίνησα τη Δευτέρα το πρωί στις 7:15 και κατάφερα να φτάσω στη Θεσσαλονίκη στις 12:15. Την επόμενη μέρα ξεκίνησα το ταξίδι της επιστροφής για Αθήνα. Δεν βιαζόμουν καθόλου, οπότε έφυγα στις 9:00 το πρωί και πήρα τον ίδιο δρόμο που είχα έρθει. Επέστρεψα στην Αθήνα στις 16:00 το απόγευμα, γιατί έκανα και δύο στάσεις για καφέ και φαγητό.
Ποια είναι η πιθανότητα να βρέθηκα στο ίδιο σημείο της διαδρομής (από την αντίθετη βέβαια πλευρά του δρόμου) ακριβώς την ίδια ώρα της ημέρας;

Λύση

Σ' ένα μοναστήρι υπάρχει ένας τεράστιος διάδρομος που φωτίζεται με 1000 διαδοχικά τοποθετημένα φώτα. Κάτω από το καθένα κρέμεται ένα κορδόνι που ανοίγει και κλείνει το αντίστοιχο φως.
Κάθε δέκα χρόνια ένας μοναχός ακολουθεί την εξής ιεροτελεστία:
Αρχικά όλα τα φώτα είναι σβηστά. Την πρώτη μέρα περνάει από τον διάδρομο και τραβάει όλα τα κορδόνια. Έτσι ανάβουν όλα τα φώτα του. Τη δεύτερη μέρα τραβάει κάθε δεύτερο κορδόνι, δηλαδή σβήνει τα φώτα Νο 2, 4, 6, 8, κλπ. Την τρίτη μέρα τραβάει κάθε τρίτο κορδόνι, δηλαδή αυτό που αντιστοιχεί στα φώτα Νο 3, 6, 9, κλπ.
Τη διαδικασία αυτή την επαναλαμβάνει μέχρις ότου τραβήξει μόνο το κορδόνι του φωτός Νο 1000.
Εκείνη την ημέρα ποια φώτα θα είναι αναμμένα;
Κι ένα πιο δύσκολο ερώτημα: Δώστε μια μαθηματική εξήγηση γιατί θα είναι μόνο αυτά.

Λύση

Σ' ένα στρατόπεδο συγκέντρωσης Γερμανών κατά τον Β' Παγκόσμιο Πόλεμο, ο συνταγματάρχης των Ες-Ες μπαίνει το βράδυ στο κατάλυμα που βρίσκονται 100 κρατούμενοι και τους φέρνει ένα καλάθι με 100 σκουφάκια, εκ των οποίων τα 50 είναι άσπρα και τ' άλλα 50 μαύρα. Επικρατεί απόλυτο σκοτάδι μέσα στο κατάλυμα κι έτσι οι κρατούμενοι δεν μπορούν να δουν τίποτα.
Με το όπλο λοιπόν στο χέρι, τους διατάζει να πάρει ο καθένας τους από το καλάθι ένα σκουφάκι, να το φορέσει στο κεφάλι του (χωρίς να ξέρουν τι χρώμα φορούν) και να στοιχιθούν στην αυλή σε ΜΙΑ ΣΕΙΡΑ, ο ένας πλάι στον άλλον, ούτως ώστε να βρεθούν στο αριστερό άκρο αυτοί με τα μαύρα σκουφάκια και στο δεξί άκρο αυτοί με τα άσπρα ή το αντίστροφο. Σημειωτέον ότι στο στρατόπεδο δεν υπάρχουν καθόλου ανακλαστικά αντικείμενα ώστε να μπορεί κάποιος να καθρεπτιστεί μέσα σ' αυτά (π.χ. καθρέπτες, λακκούβες με νερό κλπ.), για να δει τι χρώμα σκουφάκι φοράει. Απαγορεύεται να επικοινωνήσουν μεταξύ τους με οποιονδήποτε τρόπο και επίσης απαγορεύεται να δημιουργήσουν και δεύτερη σειρά.
Σε περίπτωση που δεν θα κατάφερναν να πραγματοποιήσουν την εντολή του (να χωριστούν οι 50 με μαύρα σκουφάκια από τους 50 με άσπρα), θα τους σκότωνε όλους.
Φορούν λοιπόν οι κρατούμενοι τα σκουφάκια τους και βγαίνουν στο προαύλιο, όπου υπήρχε λίγο φως και μπορούσαν να δουν τι χρώμα σκουφάκι φορούσαν οι υπόλοιποι, χωρίς φυσικά να τους το πουν ή να τους κάνουν οποιοδήποτε νόημα. Όταν βγήκε κι ο τελευταίος, ο σαδιστής συνταγματάρχης αντικρίζει με μεγάλη του έκπληξη μία σειρά από 100 κρατούμενους εκ των οποίων οι πρώτοι 50 φορούσαν μαύρα σκουφάκια και οι επόμενοι 50 φορούσαν άσπρα.
Πώς κατάφεραν οι κρατούμενοι και μοιράστηκαν μ' αυτόν τον τρόπο;

Λύση

Παίζεις το παρακάτω παιχνίδι με έναν φίλο σου:
Βάζετε μπροστά σας 21 σπίρτα και ο καθένας με τη σειρά του παίρνει από 1 έως 3 από τα σπίρτα αυτά. Νικητής είναι αυτός που θα πάρει το τελευταίο σπίρτο. Αν ξεκινάς πρώτος, με ποια στρατηγική θα κερδίσεις στα σίγουρα το παιχνίδι;

Λύση

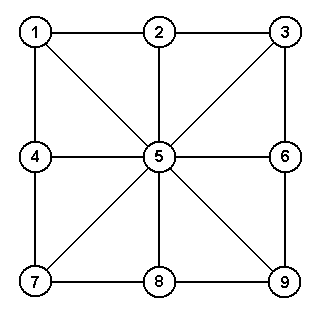
Τοποθετούμε εννέα νομίσματα έτσι ώστε να σχηματίζουν 3 οριζόντιες, 3 κάθετες και 2 διαγώνιες ευθείες νομισμάτων, κάθε μία από τις οποίες περιλαμβάνει τρία νομίσματα, σύμφωνα με την εικόνα. Το σύνολο των ευθειών αυτών είναι 8.
Μπορείτε να αναδιατάξετε κάποια νομίσματα έτσι ώστε να σχηματίζουν 10 ευθείες των τριών νομισμάτων η κάθε μία;
Η λύση του προβλήματος δεν έχει κανένα απολύτως κόλπο. Κατασκευάζεται στο επίπεδο όπως και αυτή των 8 ευθειών και γενικά ακολουθεί ακριβώς τους ίδιους κανόνες.

Λύση

Θέλεις να φτιάξεις ένα ημερολόγιο το οποίο θα δείχνει την ημέρα του μήνα με ένα σύστημα δύο κύβων τοποθετημένων δίπλα-δίπλα, οι οποίοι στην κάθε έδρα τους θα έχουν από ένα ψηφίο. Έτσι π.χ. η 3η του μηνός συμβολίζεται σαν "03", γυρνώντας τον πρώτο κύβο να δείχνει το ψηφίο 0 και τον δεύτερο να δείχνει το ψηφίο 3. Είναι άραγε δυνατή μια τέτοια κατασκευή, ώστε να απεικονίζονται σωστά όλες οι ημερομηνίες από 01 έως 31 του μηνός; Ποιο ψηφίο θα πρέπει να βάλεις σε κάθε έδρα του κάθε κύβου;

Λύση

Ένα φορτηγό ξεκινάει από το κάτω μέρος ενός ανηφορικού δρόμου και θέλει να ανεβάσει 10 βαρέλια γεμάτα με πετρέλαιο στο πάνω μέρος του δρόμου. Μπορεί να μεταφέρει μόνο ένα βαρέλι κάθε φορά. Το φορτηγό δεν έχει ρεζερβουάρ και για να ανέβει την ανηφόρα συνδέει το βαρέλι που μεταφέρει με τον κινητήρα του και καίει το πετρέλαιο του βαρελιού. Για να ανέβει από τη βάση του δρόμου ως την κορυφή του, χρειάζεται να καταναλώσει ακριβώς το περιεχόμενο ενός βαρελιού.
Διευκρίνηση: Το φορτηγό μπορεί να κάνει όσες στάσεις θέλει και να φορτώσει ή να ξεφορτώσει βαρέλια. Στην επιστροφή δεν καίει πετρέλαιο γιατί ο δρόμος είναι κατηφορικός. Έστω πως ο οδηγός γνωρίζει πως το συνολικό μήκος της διαδρομής είναι x μέτρα.

Ερώτημα απλούστερο: Μπορεί να ανεβάσει κάποια ποσότητα πετρελαίου μέχρι πάνω και με ποιον τρόπο;
Ερώτημα δύσκολο: Ποια είναι η μέγιστη δυνατή ποσότητα πετρελαίου που μπορεί να ανεβάσει;

Λύση

Δουλεύεις σ' ένα εστιατόριο και ο συνάδελφός σου σε προκαλεί σ' ένα παιχνίδι από το οποίο ο χαμένος θα πλύνει τα πιάτα στο τέλος της βάρδιας: Τοποθετείτε εναλλάξ έναν μεγάλο αριθμό ίδιων πιάτων οπουδήποτε πάνω σ' ένα στρογγυλό τραπέζι και ο πρώτος που δεν θα έχει χώρο για να τοποθετήσει το πιάτο του, χάνει το παιχνίδι. Τα πιάτα πρέπει να ακουμπάνε κανονικά πάνω στο τραπέζι και δεν επιτρέπεται να επικαλύπτονται μεταξύ τους. Θα διαλέξεις να παίξεις πρώτος ή δεύτερος; Ποια στρατηγική θ' ακολουθήσεις για να κερδίσεις στα σίγουρα το παιχνίδι;

Λύση

Ένας οδηγός λεωφορείου βρήκε έναν τρόπο για να καλύψει όλη την παρακάτω διαδρομή, ξεκινώντας από το σημείο Α και καταλήγοντας στο σημείο Β, χωρίς να περάσει δύο φορές από τον ίδιο δρόμο και χωρίς να διασταυρωθεί με ένα κομμάτι διαδρομής που έχει ήδη καλύψει. Μπορείτε να τον βρείτε;

Λύση

Εχουμε δύο φιτίλια με ελεύθερα τα άκρα τους, χωρίς δηλαδή να συνδέονται σε κερί. Κάθε φιτίλι καίγεται σε μία ώρα. Έχουν όμως διαφορετικό μήκος και πλάτος το καθένα, ενώ η πυκνότητα του κάθε φιτιλιού δεν είναι η ίδια σε κάθε σημείο του. Έχουμε και έναν αναπτήρα με τον οποίο μπορούμε να τα ανάψουμε. Μπορείτε να μετρήσετε ακριβώς 45 λεπτά;

Διευκρινίσεις:
1) Διαφορετική πυκνότητα σε κάθε σημείο του φιτιλιού σημαίνει πως δεν μπορούμε να το κόψουμε στη μέση και να μετρήσουμε έτσι μισή ώρα.
2) Ο χρόνος μετράται αποκλειστικά καίγοντας φιτίλια. Δεν διαθέτουμε κανένα άλλο μέσο μέτρησης χρόνου.

Λύση

Έχουμε ένα μπουκάλι κρασί βουλωμένο με φελλό, έτσι ώστε το πάνω μέρος του φελλού να φτάνει μέχρι το χείλος του μπουκαλιού. Πώς θα πιούμε το κρασί αν δεν έχουμε κανένα εργαλείο και χωρίς να σπάσουμε το μπουκάλι;

Λύση

Ένας ψαράς θέλει να ταξιδέψει αεροπορικώς μεταφέροντας μαζί του ένα καλάμι ψαρέματος. Δυστυχώς ο υπεύθυνος της εταιρίας του λέει πως το καλάμι του έχει 5 εκατοστά μεγαλύτερο μήκος από αυτό που επιτρέπουν οι κανονισμοί. Ο ψαράς μελέτησε το πρόβλημα και βρήκε έναν τρόπο για να το συσκευάσει χωρίς να το λυγίσει ή να το κοντύνει και χωρίς να παραβεί τους κανονισμούς. Τι έκανε;

Λύση

Έχουμε επτά μαγικά κεριά τοποθετημένα κυκλικά. Όλα τους είναι αναμμένα. Αυτό που τα κάνει μαγικά είναι ότι όταν φυσάμε για να σβήσουμε ένα από αυτά, σβήνουν επίσης το αριστερό και το δεξί από αυτό. Ομοίως όταν φυσάμε ένα σβηστό κερί, ανάβει τόσο αυτό όσο και τα δύο πλαϊνά του. Εάν το ένα από τα δύο πλαϊνά είναι αναμμένο και το άλλο σβηστό, θα σβήσει το πρώτο και θ' ανάψει το δεύτερο. Γενικά ισχύει ότι φυσώντας οποιοδήποτε κερί, αλλάζει η κατάσταση τόσο αυτού όσο και των δύο πλαϊνών του. Πώς θα μπορέσουμε να τα σβήσουμε όλα;

Λύση

Ένας κυνηγός ξεκινάει από τον καταυλισμό του και περπατάει ένα χιλιόμετρο νότια για να κυνηγήσει αρκούδες. Ξαφνικά βλέπει μια αρκούδα, η οποία όμως τον αντιλήφθηκε και άρχισε να τρέχει ανατολικά. Ο κυνηγός την κυνήγησε για ένα χιλιόμετρο αλλά δεν κατόρθωσε να την προλάβει. Απογοητευμένος περπάτησε ένα χιλιόμετρο βόρεια και ξαναγύρισε στον καταυλισμό του. Τι χρώμα είχε η αρκούδα;

Λύση

Πόσες φορές συναντώνται μέσα σε διάστημα δώδεκα ωρών ο ωροδείκτης και ο λεπτοδείκτης ενός ρολογιού;

Λύση

Ένας άνθρωπος περπατώντας στον δρόμο συναντά μια νεκροφόρα στην οποία υπάρχει ένα φέρετρο και ο οδηγός της οδηγεί κλαίγοντας. Τον ρωτάει λοιπόν αν είχε καμιά συγγένεια με τον νεκρό και εκείνος του απαντάει: "Αδελφούς και αδελφές δεν έχω. Αλλά ο πατέρας του νεκρού, είναι γιος του πατέρα μου". Τι συγγένεια είχε ο οδηγός με τον νεκρό;

Λύση

Ένας πατέρας με τον γιο του ξεκινούν μαζί για έναν περίπατο πατώντας ταυτόχρονα το δεξί τους πόδι πρώτα. Από εκεί και μετά, για κάθε δύο βήματα του πατέρα, το παιδί κάνει τρία. Πότε θα πατήσουν ταυτόχρονα το αριστερό τους πόδι;

Λύση