 Όλοι οι κύκλοι έχουν ίσες περιφέρειες (*)
Όλοι οι κύκλοι έχουν ίσες περιφέρειες (*)
 Όλοι οι κύκλοι έχουν ίσες περιφέρειες (*)
Όλοι οι κύκλοι έχουν ίσες περιφέρειες (*)
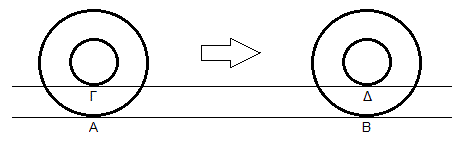
Στο σχήμα φαίνεται ένας δίσκος που έχει πάνω του χαραγμένους δύο κύκλους και απεικονίζεται στην αρχική και στην τελική του θέση μετά από μια πλήρη κύλισή του. Το σημείο Α του εξωτερικού κύκλου καταλήγει στο σημείο Β και το σημείο Γ του εσωτερικού κύκλου καταλήγει στο σημείο Δ. Αφού η περιστροφή είναι πλήρης, η απόσταση ΑΒ ισούται με την περιφέρεια του μεγάλου κύκλου και η απόσταση ΓΔ ισούται με την περιφέρεια του μικρού κύκλου. Όμως οι αποστάσεις ΑΒ και ΓΔ είναι προφανώς ίσες, οπότε οι δύο κύκλοι έχουν ίσες περιφέρειες.
Όλα τα άλογα έχουν το ίδιο χρώμα (***)
Θα αποδείξουμε πως όλα τα άλογα έχουν το ίδιο χρώμα. Ξεκινάμε με την πρόταση:
ν άλογα έχουν πάντοτε το ίδιο χρώμα.
Αρκεί να αποδείξουμε πως η παραπάνω πρόταση είναι αληθής για κάθε ν. Αυτό θα το επιτύχουμε με τη διαδικασία της Επαγωγής, ως εξής:
1) Επαληθεύουμε την Πρόταση για ν=1. Πράγματι, ένα άλογο έχει πάντοτε το ίδιο χρώμα με τον εαυτό του.
2) Υποθέτουμε ότι η πρόταση ισχύει για ν άλογα.
3) Θα αποδείξουμε πως η πρόταση ισχύει για ν+1 άλογα:
Έστω πως έχουμε μια ομάδα ν+1 αλόγων. Ονομάζουμε το πρώτο άλογο της ομάδας Π και το τελευταίο άλογο της ομάδας Τ.
Αφαιρούμε το άλογο Π από την ομάδα και αυτά που μένουν είναι ν στον αριθμό. Άρα από την υπόθεση που κάναμε στο βήμα 2, πρέπει να έχουν όλα το ίδιο χρώμα. Οπότε το άλογο Τ έχει το ίδιο χρώμα με τα υπόλοιπα.
Βάζουμε το άλογο Π στη θέση του και αφαιρούμε το άλογο Τ από την ομάδα. Μένουν πάλι ν άλογα που έχουν όλα το ίδιο χρώμα. Οπότε το άλογο Π έχει το ίδιο χρώμα με τα υπόλοιπα.
Αφού τόσο το άλογο Τ όσο και το άλογο Π έχουν το ίδιο χρώμα με τα υπόλοιπα, πρέπει να έχουν το ίδιο χρώμα και μεταξύ τους.
Άρα και τα ν+1 άλογα έχουν όλα το ίδιο χρώμα.
Αποδείξαμε με τη διαδικασία της Επαγωγής πως όλα τα άλογα έχουν το ίδιο χρώμα. Που βρίσκεται το λάθος στον παραπάνω συλλογισμό;
Το παράδοξο της Ωραίας Κοιμωμένης (*****)
Η Ωραία Κοιμωμένη δέχτηκε να συμμετάσχει στο παρακάτω πείραμα:
Την Κυριακή θα πάρει μία δόση υπνωτικού και θα πέσει για ύπνο. Ενώ κοιμάται, ένας ερευνητής θα στρίψει ένα νόμισμα.
Αν το νόμισμα έρθει Κορώνα, θα ξυπνήσει την Κοιμωμένη τη Δευτέρα και θα της κάνει την ερώτηση: «ποια είναι η πιθανότητα το νόμισμα που έστριψα να έφερε Κορώνα;». Η Κοιμωμένη θα δώσει την απάντησή της και το πείραμα θα τελειώσει.
Αν το νόμισμα έρθει Γράμματα, θα ξυπνήσει πάλι την Κοιμωμένη τη Δευτέρα και θα της κάνει την ίδια ερώτηση. Η Κοιμωμένη θα απαντήσει, αλλά στη συνέχεια θα της χορηγήσει άλλη μια δόση του υπνωτικού που θα την κοιμίσει μέχρι την Τρίτη. Τότε θα την ξυπνήσει πάλι και θα της επαναλάβει για δεύτερη φορά την ίδια ερώτηση. Η Κοιμωμένη θα απαντήσει και το πείραμα θα τελειώσει.
Η Κοιμωμένη γνωρίζει ακριβώς τους όρους του πειράματος, αλλά σε κανένα ξύπνημά της δεν γνωρίζει τι μέρα είναι, ούτε θυμάται αν έχει ξυπνήσει ξανά.
Ποια είναι η σωστή απάντηση που πρέπει να δώσει μόλις ξυπνήσει;
Το πρόβλημα έχει διχάσει τις γνώμες έμπειρων γριφολυτών, μαθηματικών και φιλοσόφων. Υπάρχουν τρεις διαφορετικές σχολές σκέψης: Οι halfers, που υποστηρίζουν πως η πιθανότητα είναι 1/2, οι thirders που υποστηρίζουν πως η πιθανότητα είναι 1/3 και οι ουδέτεροι που υποστηρίζουν πως το πρόβλημα δεν έχει ξεκάθαρη λύση γιατί δεν ορίζεται επαρκώς. Αυτός είναι ο λόγος που έχει χαρακτηριστεί παράδοξο, ενώ η διαμάχη των halfers με τους thirders συνεχίζεται μέχρι και σήμερα.
Πέντε προτάσεις (**)
Διαβάστε τις παρακάτω πέντε προτάσεις και αποφασίστε ποιες από αυτές είναι αληθείς και ποιες ψευδείς:
Η επόμενη πρόταση είναι αληθής.
Η επόμενη πρόταση είναι ψευδής.
Η επόμενη πρόταση είναι αληθής.
Η επόμενη πρόταση είναι ψευδής.
Η πρώτη πρόταση είναι αληθής.
Στη συνέχεια κάντε το ίδιο και για τις παρακάτω πέντε προτάσεις:
Η επόμενη πρόταση είναι ψευδής.
Η επόμενη πρόταση είναι αληθής.
Η επόμενη πρόταση είναι ψευδής.
Η επόμενη πρόταση είναι αληθής.
Η πρώτη πρόταση είναι ψευδής.
Παρατηρείτε μια ουσιαστική διαφορά μεταξύ των δύο ομάδων προτάσεων; Πού οφείλεται;
Όλα τα τρίγωνα είναι ισοσκελή (**)
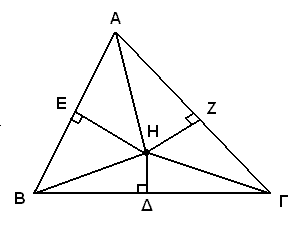
1. Κατασκευάζουμε ένα τυχαίο τρίγωνο ΑΒΓ.
2. Φέρνουμε τη διχοτόμο της γωνίας Α και τη μεσοκάθετη της πλευράς ΒΓ. Το σημείο που τέμνονται το ονομάζουμε Η. Από το σημείο Η φέρνουμε κάθετες και προς τις άλλες δύο πλευρές.
3. Τα ορθογώνια τρίγωνα ΑΕΗ και ΑΖΗ είναι ίσα, επειδή έχουν ίση τη μισή γωνία Α και την πλευρά ΑΗ κοινή. Άρα ΑΕ = ΑΖ (1).
4. Τα ορθογώνια τρίγωνα ΒΔΗ και ΓΔΗ είναι ίσα, επειδή έχουν ΒΔ = ΔΓ και την πλευρά ΗΔ κοινή. Άρα ΗΒ = ΗΓ.
5. Τα ορθογώνια τρίγωνα ΒΕΗ και ΓΖΗ είναι ίσα, επειδή έχουν ΗΒ = ΗΓ (από το Βήμα 4) και ΕΗ = ΗΖ (από το Βήμα 3). Άρα ΕΒ = ΖΓ (2).
6. Με πρόσθεση κατά μέλη των (1) και (2) προκύπτει πως ΑΒ = ΑΓ.
7. Άρα το τυχαίο τρίγωνο είναι ισοσκελές.
Που βρίσκεται το λάθος;
Ανταλλαγή φακέλων (****)
Η Αλίκη και ο Βασίλης τραβάνε στην τύχη από έναν κλειστό φάκελο ο καθένας. Ο οργανωτής του παιχνιδιού τους λέει πως ο κάθε φάκελος έχει μέσα ένα χρηματικό ποσό το οποίο το έχουν ήδη κερδίσει. Τους λέει επίσης ότι ο ένας φάκελος έχει το διπλάσιο ποσό από τον άλλον, χωρίς να τους αποκαλύψει ποιος. Στη συνέχεια τους δίνεται το δικαίωμα αν θέλουν να ανταλλάξουν μεταξύ τους φακέλους.
Η Αλίκη υπολογίζει το κέρδος που αναμένεται να έχει αν δεχτεί να αλλάξει φακέλους ως εξής:
Αν x είναι το ποσό που έχει μέσα ο φάκελός της, τότε με πιθανότητα 1/2 διπλασιάζει το ποσό της, οπότε θα έχει κέρδος x, ενώ με πιθανότητα 1/2 υποδιπλασιάζει το ποσό της, οπότε θα έχει κέρδος –x/2. Σύμφωνα με αυτόν τον συλλογισμό το αναμενόμενο κέρδος της είναι:
(1/2) * x + (1/2) * –x/2 = x/4.
Άρα έχει 25% αναμενόμενο κέρδος αν αλλάξει φακέλους και συνεπώς δέχεται να κάνει την αλλαγή.
Τον ίδιο συλλογισμό κάνει και ο Βασίλης από τη δική του πλευρά και καταλήγει φυσικά στο ίδιο συμπέρασμα, ότι δηλαδή τον συμφέρει κι αυτόν να αλλάξει φακέλους.
Έτσι πραγματοποιείται η αλλαγή. Πριν όμως ανοίξουν τους φακέλους τους και αποκαλυφθούν τα ποσά που κρύβουν, η Αλίκη επαναλαμβάνει τον συλλογισμό της και βρίσκει πως η εκ νέου αλλαγή φακέλων θα της αποφέρει ένα επιπλέον κέρδος λίγο μεγαλύτερο του 25%, το οποίο προκύπτει αν αντί του x στον τύπο βάλουμε το x + x/4 που είναι το ποσό που αναμένει να έχει τώρα στον φάκελό της. Το ίδιο υπολογίζει και ο Βασίλης, οπότε ξανα-αλλάζουν φακέλους και ο καθένας τους θεωρεί πως τώρα έχει ένα αναμενόμενο κέρδος λίγο μεγαλύτερο του 50%. Με το ίδιο σκεπτικό συνεχίζουν να αλλάζουν φακέλους μέχρι να γίνουν και οι δύο πάμπλουτοι.
Στην παραπάνω λογική κάτι πρέπει να πηγαίνει τελείως λάθος, αλλά τι ακριβώς;
Το παράδοξο της Αγίας Πετρούπολης (****)
Κάποιος σας προτείνει να παίξετε ένα παιχνίδι τύχης με τους εξής όρους: Θα ρίχνετε συνεχώς ένα νόμισμα μέχρι αυτό να φέρει για πρώτη φορά Κορώνα. Αν αυτό συμβεί με την πρώτη σας προσπάθεια θα σας δώσει 2 ευρώ και το παιχνίδι θα τελειώσει. Αν συμβεί με τη δεύτερη προσπάθειά σας θα σας δώσει 4 ευρώ. Αν συμβεί με την τρίτη θα σας δώσει 8 ευρώ και γενικά όσο περισσότερο καθυστερεί η εμφάνιση της πρώτης Κορώνας, τόσο αυτός θα διπλασιάζει το ποσό που θα κερδίσετε. Το ερώτημα είναι ποιο είναι το μέγιστο ποσό που διατίθεστε να πληρώσετε σαν εισιτήριο για να συμμετάσχετε στο παιχνίδι;
Ας προσπαθήσουμε να δώσουμε μια μαθηματική απάντηση στο πρόβλημα στην περίπτωση που ο διοργανωτής σας έλεγε πως θα ρίξετε το νόμισμα μία φορά και αν δεν φέρετε Κορώνα δεν θα πάρετε τίποτα. Τότε το αναμενόμενο κέρδος σας θα ήταν:
1/2 * 2 ευρώ + 1/2 * 0 ευρώ = 1 ευρώ και άρα μέχρι 1 ευρώ θα σας συνέφερε να πληρώσετε σαν εισιτήριο για να παίξετε.
Αν ο διοργανωτής σας έλεγε πως θα ρίξετε το νόμισμα μέχρι δύο φορές το πολύ και αν δεν φέρετε Κορώνα μέχρι τότε δεν θα πάρετε τίποτα, τότε το αναμενόμενο κέρδος σας θα ήταν:
1/2 * 2 ευρώ + 1/2 * (1/2 * 4 ευρώ + 1/2 * 0 ευρώ) = 2 ευρώ και άρα μέχρι 2 ευρώ θα σας συνέφερε να πληρώσετε σαν εισιτήριο για να παίξετε.
Γενικεύοντας, γίνεται φανερό πως αν ο διοργανωτής σας έλεγε πως θα ρίξετε το νόμισμα μέχρι Ν φορές το πολύ, τότε θα σας συνέφερε να πληρώσετε μέχρι Ν ευρώ για να συμμετάσχετε στο παιχνίδι.
Στην πραγματική περίπτωση ο διοργανωτής δεν έθεσε περιορισμό για το μέχρι πόσες φορές μπορείτε να ρίξετε το νόμισμα και αυτό εξαρτάται μόνο από το πότε θα έρθει η πρώτη Κορώνα. Επειδή η πρώτη Κορώνα μπορεί να καθυστερήσει απεριόριστες επαναλήψεις να εμφανισθεί, προκύπτει πως σαν συμφέρει να πληρώσετε ένα απεριόριστα μεγάλο ποσό για να συμμετάσχετε στο παιχνίδι.
Παρ' όλ' αυτά, είναι απίθανο κάποιος να δεχτεί να πληρώσει περισσότερα από 10 ευρώ περίπου για να παίξει. Που νομίζετε ότι οφείλεται αυτή η τεράστια διαφορά μεταξύ του μαθηματικού υπολογισμού και της ανθρώπινης διαίσθησης;
Ανακατασκευή τετραγώνου (****)
Παίρνουμε ένα τετράγωνο χαρτόνι και το διαγραμμίζουμε σε οκτώ επί οκτώ ίσα μικρότερα τετράγωνα, σαν σκακιέρα. Στη συνέχεια κόβουμε το χαρτόνι πάνω στις γραμμές που φαίνονται στο πρώτο σχήμα.
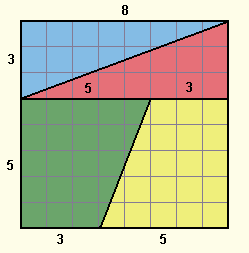
Αναδιατάσσουμε τα κομμάτια ώστε να σχηματίσουμε ένα νέο σχήμα που είναι ένα ορθογώνιο παραλληλόγραμμο με διαστάσεις 13 x 5, όπως φαίνεται στο δεύτερο σχήμα.
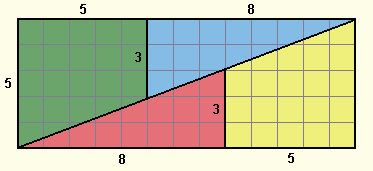
Το αρχικό τετράγωνο αποτελούνταν από 8 x 8 = 64 μικρότερα τετράγωνα, ενώ το νέο σχήμα αποτελείται από 13 x 5 = 65 τετράγωνα. Πώς προέκυψε αυτό το επιπλέον τετραγωνάκι;
Το παράδοξο του Russell (*****)
Σε μια βιβλιοθήκη υπάρχουν κάποιοι κατάλογοι που περιέχουν τίτλους βιβλίων σχετικών με κάποιο θέμα.
Για την καλύτερη εξυπηρέτηση των αναγνωστών, υπάρχουν και κάποιοι πιο γενικοί κατάλογοι οι οποίοι περιέχουν τίτλους των προηγούμενων καταλόγων αναλόγως με το θέμα στο οποίο αναφέρονται.
Από λάθος όμως, μερικοί από αυτούς τους γενικούς καταλόγους περιέχουν και τον τίτλο του εαυτού τους. Όταν ο υπεύθυνος της βιβλιοθήκης αντιλήφθηκε το λάθος αποφάσισε να φτιάξει έναν νέο κατάλογο, τον οποίο ονόμασε «Κατάλογος Σωστών Καταλόγων» και ο οποίος θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
Και εδώ εμφανίζεται το παράδοξο: Θα πρέπει να συμπεριλάβει στον νέο κατάλογό του τον καινούργιο τίτλο; Αν τον συμπεριλάβει τότε θα περιέχει τον εαυτό του και άρα δεν θα είναι σωστός κατάλογος. Αν δεν τον συμπεριλάβει τότε ο νέος κατάλογος δεν θα περιέχει όλους τους τίτλους των γενικών καταλόγων που δεν περιέχουν τον εαυτό τους.
Το παράδοξο του Ζήνωνα (*)
Ο Αχιλλέας έκανε αγώνα δρόμου με μια χελώνα. Επειδή όμως ήταν σαφώς πιο γρήγορος από αυτήν, ξεκίνησαν με μια απόσταση μεταξύ τους S0. Όταν ο Αχιλλέας έφτασε στο σημείο που βρισκόταν αρχικά η χελώνα, αυτή στο μεταξύ είχε προχωρήσει κατά μια απόσταση S1. Όταν ο Αχιλλέας κάλυψε την απόσταση S1, η χελώνα είχε στο μεταξύ προχωρήσει κατά μια μικρότερη απόσταση S2.
Επαναλαμβάνοντας αυτή τη διαδικασία φαίνεται πως ο Αχιλλέας δεν θα μπορούσε ποτέ να ξεπεράσει τη χελώνα. Ποια είναι η λύση αυτού του παραδόξου;
Ποιος ξυρίζει τον κουρέα; (**)
Σε ένα χωριό ισχύουν οι παρακάτω δύο κανόνες:
1) Υπάρχει μόνο ένας κουρέας
2) Ο κάθε κάτοικος είτε ξυρίζεται μόνος του είτε τον ξυρίζει ο κουρέας
Το ερώτημα που προκύπτει είναι ποιος ξυρίζει τον κουρέα;
- Αν ξυρίζεται μόνος του τότε δεν τον ξυρίζει ο κουρέας, πράγμα άτοπο, γιατί ο ίδιος είναι κουρέας.
- Αν τον ξυρίζει κάποιος άλλος τότε αυτός ο άλλος πρέπει να είναι κουρέας, πράγμα άτοπο γιατί υπάρχει μόνο ένας κουρέας.
Το διαγώνισμα έκπληξη (**)
Μια Παρασκευή μεσημέρι λέει η δασκάλα στους μαθητές της ότι την επόμενη εβδομάδα θα τους βάλει ένα διαγώνισμα έκπληξη, δηλαδή δεν θα το περιμένουν.
Αφού βγαίνει από την αίθουσα οι μαθητές κάθονται και σκέφτονται ψύχραιμα πως αν το διαγώνισμα δεν έχει μπει μέχρι την ερχόμενη Πέμπτη, τότε η μόνη διαθέσιμη μέρα για να μπει θα είναι η Παρασκευή. Τότε όμως όλοι θα το περιμένουν και άρα δεν θα είναι πια έκπληξη, οπότε η δασκάλα δεν μπορεί να βάλει το διαγώνισμα την Παρασκευή.
Αν περάσει η Τετάρτη και το διαγώνισμα δεν έχει μπει, τότε με δεδομένο ότι δεν μπορεί να μπει ούτε την Παρασκευή, θα πρέπει αναγκαστικά να μπει την Πέμπτη. Και πάλι όμως τότε όλοι θα το περιμένουν, οπότε ούτε και την Πέμπτη μπορεί να μπει το διαγώνισμα.
Συνεχίζοντας αυτή τη συλλογιστική, αποκλείονται μία-μία όλες οι μέρες της εβδομάδας και άρα η δασκάλα δεν μπορεί καμία μέρα να βάλει το διαγώνισμα έκπληξη.
Πώς εξηγείται αυτό το παράδοξο;
Το παράδοξο του Πρωταγόρα (***)
Στον Πρωταγόρα αποδίδεται το παρακάτω θεωρητικό παράδοξο:
Ο Αρίστιππος ζήτησε από τον Πρωταγόρα να του διδάξει Νομική. Επειδή όμως δεν είχε λεφτά να τον πληρώσει, συμφώνησαν ο Πρωταγόρας να πληρωθεί μόλις ο Αρίστιππος κερδίσει την πρώτη του δίκη.
Ο Αρίστιππος όμως δεν τα κατάφερνε καθόλου καλά στο δικαστήριο και έτσι ο Πρωταγόρας του ζήτησε την καταβολή των χρημάτων του, παρόλο που δεν είχε κερδίσει ακόμα καμία δίκη. Ο Αρίστιππος αρνήθηκε επικαλούμενος τη συμφωνία τους και το θέμα έφτασε στα δικαστήρια.
Ο δικαστής που άκουσε την υπόθεση βρέθηκε στο παρακάτω λογικό παράδοξο:
Αν δικαίωνε τον Αρίστιππο με απόφαση να μην πληρώσει τον Πρωταγόρα τότε ο Αρίστιππος θα είχε μόλις κερδίσει την πρώτη του δίκη και για το λόγο αυτό θα έπρεπε να πληρώσει τον Πρωταγόρα.
Αν από την άλλη, δικαίωνε τον Πρωταγόρα με απόφαση να πληρωθεί από τον Αρίστιππο τότε ο τελευταίος δεν θα είχε κερδίσει ακόμα την πρώτη του δίκη και έτσι δεν θα έπρεπε να πληρώσει τον Πρωταγόρα.
Πώς θα βγει ο δικαστής από αυτό το αδιέξοδο;
Άτοπη εξίσωση (**)
Ξεκινώντας από την υπόθεση ότι α=β και με μια σειρά συνεπαγωγών καταλήγουμε στο αποτέλεσμα ότι 2=1. Που βρίσκεται το λάθος;
α=β \Leftrightarrow α^2=αβ \Leftrightarrow α^2-β^2=αβ-β^2 \Leftrightarrow (α+β)(α-β)=β(α-β) \Leftrightarrow 2β(α-β)=β(α-β) \Leftrightarrow 2β=β \Leftrightarrow 2=1
Παράδοξο της διαγωνίου (*)
Έχουμε ένα τετράγωνο πλευράς 1 μέτρου και πρέπει να ενώσουμε με το μολύβι τις δύο απέναντι κορυφές του. Μπορούμε μόνο να φέρνουμε ευθύγραμμα τμήματα, όσο μικρά θέλουμε, που όμως πρέπει να είναι παράλληλα ή κάθετα με τις πλευρές του τετραγώνου.
Ο πιο απλός τρόπος είναι να φέρουμε πρώτα μια ευθεία πάνω στη βάση του και μετά μία πάνω στο ύψος του. Έτσι το συνολικό μήκος της γραμμής που φέραμε είναι 2 μέτρα.
Είναι αξιοσημείωτο ότι όσο μικρά κι αν είναι τα ευθύγραμμα τμήματα που φέρνουμε, το συνολικό τους μήκος είναι πάντα 2 μέτρα, όπως φαίνεται στο σχήμα για τμήματα που ισούνται με το 1/5 και το 1/20 της πλευράς του τετραγώνου.
Για τμήματα ίσα με το 1/100 της πλευράς ή ακόμα μικρότερα, ουσιαστικά έχουμε φέρει τη διαγώνιο του τετραγώνου. Πώς γίνεται όμως το συνολικό μήκος της γραμμής μας να είναι 2 μέτρα, αφού ως γνωστόν το μήκος της διαγωνίου είναι ρίζα 2 ;
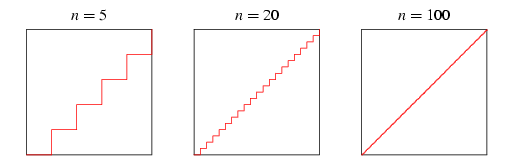
Που πήγε η γραμμή; (***)
Εάν κόψουμε το παρακάτω σχήμα κατά μήκος της διαγωνίου γραμμής και στη συνέχεια σύρουμε το επάνω τμήμα προς τα αριστερά, έτσι ώστε να συμπέσουν οι κάθετες γραμμές μεταξύ τους, θα δούμε πως οι 10 κάθετες γραμμές έγιναν τώρα 9. Που πήγε η 10η γραμμή;
Χαμένο ευρώ (****)
Τρεις φίλοι μπαίνουν σε μια κάβα και αγοράζουν ένα μπουκάλι κρασί που κοστίζει 30 ευρώ δίνοντας 10 ευρώ ο καθένας. Φεύγοντας, τους προλαβαίνει ο υπάλληλος και τους λέει πως έκανε λάθος γιατί το μπουκάλι στοιχίζει 25 και όχι 30 ευρώ και γι' αυτό τους επιστρέφει 5 ευρώ ρέστα. Αυτοί, αφού δεν μπορούν να μοιράσουν τα 5 ευρώ στα τρία, παίρνουν από 1 ευρώ ο καθένας και δίνουν 2 ευρώ φιλοδώρημα στον υπάλληλο για την καλή του πράξη. Στο τέλος όμως σκέφτονται: Έδωσε ο καθένας μας 10 ευρώ και πήρε ένα πίσω, άρα ο καθένας πλήρωσε 9 ευρώ. Τρεις φορές το 9 μας κάνει 27 και 2 ευρώ για το φιλοδώρημα, 29. Τι έγινε το ένα ευρώ;