Γρίφοι Συνδυασμών

Συνδυασμών - Ιδέα (****)

Ξεκινώντας από το κεντρικό τετράγωνο του εικονιζόμενου πίνακα με το γράμμα Ι, με πόσους διαφορετικούς τρόπους μπορείτε να γράψετε τη λέξη ΙΔΕΑ;
Από κάθε τετράγωνο μπορείτε να κινηθείτε σε οποιοδήποτε γειτονικό του τετράγωνο, οριζόντια, κάθετα ή διαγώνια.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Έξι μαθητές έχουν διαφορετικά ύψη μεταξύ τους. Με πόσους τρόπους μπορούν να στηθούν σε μία σειρά έτσι ώστε να μην υπάρχουν τρεις συνεχόμενοι μαθητές σε αύξουσα διάταξη ύψους από την αρχή προς το τέλος της σειράς;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ένας κωδικός έχει τις εξής ιδιότητες:
1. Είναι 8-ψήφιος.
2. Όλα τα ψηφία του είναι διαφορετικά μεταξύ τους.
3. Αποτελείται από τρεις 2-ψήφιους περιττούς αριθμούς και το άθροισμά τους, που βρίσκεται στα 2 πρώτα από αριστερά ψηφία.
Μπορείτε να βρείτε τα δύο πρώτα από αριστερά ψηφία του κωδικού;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Σημειώνουμε ν τελείες στα τετράγωνα ενός τετραγωνισμένου χαρτιού, μία το πολύ σε κάθε τετράγωνο, έτσι ώστε κάθε τελεία να έχει ζυγό αριθμό από τελείες-γείτονες. Δύο τελείες θεωρούνται γειτονικές αν περιέχονται σε διπλανά τετράγωνα, οριζόντια ή κάθετα αλλά όχι διαγώνια. Οι τελείες που θα σημειώσουμε θα πρέπει να σχηματίζουν μια ενιαία περιοχή, δηλαδή θα πρέπει από κάθε τελεία να μπορούμε να πάμε σε κάθε άλλη ακολουθώντας τους γείτονές της. Για παράδειγμα, η λύση για ν=4 τελείες φαίνεται στο παρακάτω σχήμα.
Για ποιες τιμές του ν το πρόβλημα δεν έχει λύση;

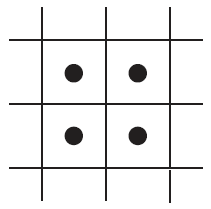
Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

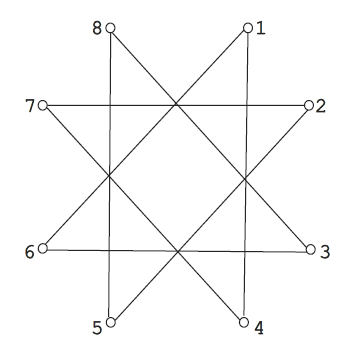
Τοποθετήστε όσο περισσότερα νομίσματα γίνεται στις κορυφές του αστεριού 8 κορυφών του σχήματος.
Ο τρόπος τοποθέτησης ενός νομίσματος σε μία κορυφή αποτελείται από 2 βήματα ως εξής: 1) Επιλέξτε μία κορυφή στην οποία δεν υπάρχει νόμισμα και τοποθετήστε σε αυτήν ένα νέο νόμισμα. 2) Σύρετε το νόμισμα που μόλις τοποθετήσατε σε μία νέα κορυφή κατά μήκος της μίας από τις δύο γραμμές του αστεριού που ξεκινούν από αυτήν την κορυφή. Η κορυφή στην οποία καταλήξατε θα πρέπει να είναι ελεύθερη και το νόμισμα που της τοποθετήσατε δεν μπορεί να μετακινηθεί ξανά.
Δώστε τις λύσεις σας στην εξής μορφή: 1->4, 2->5, κλπ., που μεταφράζεται ότι τοποθετείτε ένα νόμισμα στην κορυφή 1 και το σέρνετε στην κορυφή 4, στη συνέχεια τοποθετείτε ένα νόμισμα στην κορυφή 2 και το σέρνετε στην κορυφή 5, κλπ.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Βάζω στο μυαλό μου έναν πενταψήφιο δυαδικό αριθμό (κωδικό) και εσείς προσπαθείτε να τον βρείτε. Σε κάθε σας προσπάθεια λέτε έναν πενταψήφιο δυαδικό αριθμό και εγώ σας απαντώ πόσα ψηφία του αριθμού σας ταυτίζονται με τα ψηφία του κωδικού, χωρίς να σας αποκαλύψω ποια είναι αυτά. Π.χ. αν ο κωδικός είναι ο 01101 και εσείς μου πείτε τον αριθμό 11100 τότε θα σας απαντήσω 3, γιατί ταυτίζονται το 2ο, το 3ο και το 4ο ψηφίο των δύο αριθμών.
Πόσες το πολύ προσπάθειες θα χρειαστείτε για να βρείτε τον κωδικό; Εξαρτώνται οι αριθμοί που θα λέτε από τις απαντήσεις που θα σας δίνω; Αν όχι, ποιους αριθμούς θα μου πείτε σε κάθε σας προσπάθεια;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Θέλουμε να τοποθετήσουμε 2 βοσκούς (Β), 2 λύκους (Λ), 2 πρόβατα (Π) και δύο μαρούλια (Μ) σε μία σειρά, με τις παρακάτω δύο προϋποθέσεις:
1. Δεν επιτρέπεται δύο στοιχεία του ίδιου είδους να είναι διαδοχικά.
2. Δεν επιτρέπεται ο βοσκός να είναι δίπλα σε λύκο, ο λύκος δίπλα σε πρόβατο και το πρόβατο δίπλα σε μαρούλι.
Με αυτές τις προϋποθέσεις είναι δυνατόν να τοποθετήσουμε τα 8 στοιχεία σε μία σειρά;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Έξι χωριά βρίσκονται στις κορυφές A,B,C,D,E,F του κανονικού εξαγώνου που φαίνεται στο σχήμα. Οι γραμμές του σχήματος είναι δρόμοι που ενώνουν τα χωριά μεταξύ τους και τα ενδιάμεσα σημεία είναι διασταυρώσεις όπου μπορεί κάποιος να αλλάξει πορεία.
Τρεις γαμπροί βρίσκονται στο χωριό F και θέλουν να παντρευτούν τρεις νύφες που βρίσκονται στα χωριά E,D,C αντίστοιχα. Ο πατέρας της κάθε νύφης για να δώσει την κόρη του θέλει για προίκα τόσα ψάρια όσες και οι διαφορετικές διαδρομές που μπορεί να φτάσει ο γαμπρός από το χωριό του στο χωριό της νύφης του. Οι διαδρομές συντίθενται από τα μονοπάτια μεταξύ των διασταυρώσεων και οι διασταυρώσεις μπορούν να περιλαμβάνουν και χωριά.
Ένας γαμπρός ακολουθεί ένα μονοπάτι μόνο εάν η επόμενη διασταύρωση που θα συναντήσει βρίσκεται πιο κοντά στο χωριό της νύφης του σε σχέση με τη διασταύρωση που βρισκόταν αμέσως πριν.
Πόσα ψάρια θα πρέπει να φέρει μαζί του ο καθένας από τους τρεις γαμπρούς;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Τοποθετήστε 5 βασίλισσες σε μια σκακιέρα 5x5 έτσι ώστε να μην απειλούν 3 τετράγωνα της σκακιέρας. Δώστε τις συντεταγμένες των 3 τετραγώνων.
Σημείωση: Η βασίλισσα στο σκάκι απειλεί όλα τα τετράγωνα που βρίσκονται στην ίδια οριζόντια, κάθετη και διαγώνιο με αυτήν.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Η γιαγιά έχει 15 βάζα που το καθένα περιέχει 1,2,3,...,15 καραμέλες αντίστοιχα. Λέει στο εγγονάκι της πως κάθε μέρα μπορεί να διαλέγει όποια βάζα θέλει και να παίρνει τον ίδιο αριθμό καραμελών από κάθε βάζο που διάλεξε. Κάθε μέρα μπορεί να επιλέγει διαφορετικό αριθμό καραμελών.
Σε πόσες μέρες το λιγότερο μπορεί να καταφέρει ο μικρός να φάει όλες τις καραμέλες από όλα τα βάζα;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Βρείτε έναν εννιαψήφιο αριθμό του οποίου τα ψηφία είναι οι αριθμοί από 1 έως 9 από μία φορά ο καθένας και ο οποίος έχει την εξής ιδιότητα: Ο αριθμός πρέπει να διαιρείται ακριβώς με το 9. Αν εξαιρέσουμε το ψηφίο των μονάδων του τότε ο οκταψήφιος αριθμός που μένει πρέπει να διαιρείται ακριβώς με το 8. Αν εξαιρέσουμε το ψηφίο των μονάδων του νέου αριθμού τότε ο επταψήφιος αριθμός που μένει πρέπει να διαιρείται ακριβώς με το 7. Αυτό το μοτίβο πρέπει να ισχύει μέχρι να μείνει ένα ψηφίο στον αριθμό, το οποίο και θα διαιρείται με το 1.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ο Παύλος, ο Πέτρος και ο Θωμάς, έχουν από 8 χιτώνες ο καθένας. Κάθε ημέρα, ένας μόνο από αυτούς δίνει τους μισούς χιτώνες του σε κάποιον άλλον. Μετά από λίγες μέρες είχαν στην κατοχή τους 15, 6 και 3 χιτώνες αντίστοιχα. Τότε ο Παύλος που κρατούσε σημειώσεις, έδειξε στους άλλους δύο όλες τις μεταφορές που είχαν πραγματοποιηθεί και ο Πέτρος συμφώνησε μαζί του. Ο Θωμάς που δεν πειθόταν τόσο εύκολα, ισχυρίστηκε πως είχαν κάνει κάποιο λάθος στις μεταφορές. Ποιος έχει δίκιο;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Πέντε ζευγάρια βρίσκονται στην όχθη ενός ποταμού και θέλουν να περάσουν στην απέναντι όχθη. Έχουν στη διάθεσή τους μία βάρκα η οποία μπορεί να μεταφέρει έως τρία άτομα και για να κινηθεί χρειάζεται τουλάχιστον ένα άτομο μέσα της. Δυστυχώς οι άντρες των ζευγαριών είναι ζηλιάρηδες και δεν δέχονται επ’ ουδενί να βρεθεί η γυναίκα τους με άλλον άντρα σε κάποια όχθη, έστω και στιγμιαία, εκτός κι αν είναι και οι ίδιοι παρόντες στην ίδια όχθη. Πώς θα περάσουν και οι δέκα απέναντι και πόσες είναι οι ελάχιστες διασχίσεις του ποταμού για να τα καταφέρουν;

Οδηγίες αποστολής λύσεων: Συμβολίστε τους 5 άντρες με τα γράμματα Α-Ε και τις 5 γυναίκες με τα γράμματα α-ε. Συμβολίστε κάθε μεταβολή στη θέση των ατόμων ως προς το ποτάμι με μια νέα γραμμή κειμένου. Κάθε γραμμή κειμένου αναλύεται ως εξής: Σημειώνονται με αλφαβητική σειρά πρώτα οι άντρες που βρίσκονται στην αριστερή όχθη του ποταμού, μετά οι γυναίκες στην αριστερή όχθη, ακολουθεί μία παύλα που συμβολίζει το ποτάμι, μετά οι άντρες που βρίσκονται στη δεξιά όχθη του ποταμού και τέλος οι γυναίκες στη δεξιά όχθη. Κάθε άτομο διαχωρίζεται από το επόμενο με ένα κόμμα. Θα πρέπει το κάθε άτομο να έχει συγκεκριμένη θέση στην κάθε όχθη του ποταμού, δηλαδή αν κάποια άτομα δεν βρίσκονται σε μια δεδομένη όχθη θα πρέπει στη θέση τους να υπάρχουν κενά χωρισμένα με κόμμα.
Σαν παράδειγμα δίνονται δύο γραμμές κειμένου που συμβολίζουν την αρχική θέση των ζευγαριών και την πρώτη (προβληματική) διάσχιση του ποταμού από τους Β,Δ,γ:
Α,Β,Γ,Δ,Ε,α,β,γ,δ,ε,-, , , , , , , , , ,
Α, ,Γ, ,Ε,α,β, ,δ,ε,-, ,Β, ,Δ, , , ,γ, ,

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ