Γρίφοι Πιθανοτήτων

Memory (****)

Ένα κορίτσι παίζει Memory με τον αδελφό της. Στο παιχνίδι χρησιμοποιούνται 8 κάρτες που αποτελούνται από 4 ζευγάρια ίδιων καρτών. Στην αρχή όλες οι κάρτες είναι ανακατεμένες, κλειστές και απλωμένες σε ένα τραπέζι. Κάθε παίκτης ανοίγει διαδοχικά δύο κάρτες, τις οποίες βλέπουν και οι δύο παίκτες. Αν οι 2 κάρτες σχηματίζουν ζευγάρι τις παίρνει δίπλα του και ξαναπαίζει. Αν δεν σχηματίζουν ζευγάρι τις κλείνει πάλι και παίζει ο άλλος παίκτης. Όταν αφαιρεθούν όλες οι κάρτες από το τραπέζι, ο παίκτης που έχει πάρει τα περισσότερα ζευγάρια κερδίζει, αλλιώς το παιχνίδι λήγει ισόπαλο.
Και τα δύο παιδιά είναι ικανά να θυμούνται τις κάρτες που έχουν ανοίξει και δεν ανοίγουν μια κάρτα που έχει ανοίξει ήδη, εκτός και αν με αυτή σχηματίζεται ζευγάρι. Πρώτο θα παίξει το κορίτσι. Ποια είναι η πιθανότητα να κερδίσει το παιχνίδι;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Μια σχολική τάξη αποτελείται από 10 αγόρια και έναν αριθμό κοριτσιών. Λίγο πριν τις γιορτές προστέθηκε ένα επιπλέον παιδί στη τάξη. Μετά τις γιορτές, η τάξη έκοψε τη βασιλόπιτα της και το νόμισμα έπεσε σε αγόρι. Ποιά είναι η πιθανότητα το παιδί που προστέθηκε να ήταν αγόρι;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

10 μυρμήγκια βρίσκονται σε τυχαίες θέσεις πάνω σε ένα κυκλικό στεφάνι και κινούνται είτε δεξιόστροφα είτε αριστερόστροφα πάνω σε αυτό. Η αρχική φορά κίνησης του κάθε μυρμηγκιού είναι επίσης τυχαία. Κάθε φορά που δύο μυρμήγκια συναντιούνται αλλάζουν και τα δύο κατευθύνσεις. Όλα τα μυρμήγκια κινούνται με την ίδια σταθερή ταχύτητα και χρειάζονται 1 λεπτό για να κάνουν έναν πλήρη κύκλο του στεφανιού. Ποια είναι η πιθανότητα μετά από 1 λεπτό, το μεγαλύτερο μυρμήγκι να βρεθεί στην αρχική του θέση;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έχουμε ένα μεγάλο δοχείο, μέσα στο οποίο υπάρχουν χρωματιστά μπαλάκια διαφορετικών χρωμάτων, αλλά ίδιος αριθμός για κάθε χρώμα.
Προσθέτουμε στο δοχείο 20 μπαλάκια ενός καινούργιου χρώματος. Αν η πιθανότητα να τραβήξουμε 2 μπαλάκια ίδιου χρώματος εξακολουθεί να είναι η ίδια τόσο πριν όσο και μετά την προσθήκη, πόσα μπαλάκια υπήρχαν αρχικά στο δοχείο;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

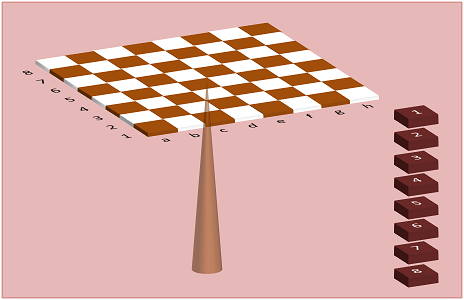
Δύο φίλοι έχουν στη διάθεσή τους τη σκακιέρα του σχήματος, η οποία ισορροπεί πάνω σε μια ακίδα που είναι τοποθετημένη στο κέντρο της. Η σκακιέρα έχει στο κάτω μέρος της 8 ταμπελάκια με τα γράμματα από το a έως το h και στο αριστερό της μέρος 8 ταμπελάκια με τους αριθμούς από το 1 έως το 8. Έχουν ακόμη 8 αριθμημένα βαρίδια (ισοβαρή και ομοιογενή), καθένα από τα οποία μπορεί να τοποθετηθεί στη σκακιέρα και να καλύψει ακριβώς ένα τετράγωνό της. Οι δύο φίλοι παίζουν το ακόλουθο παιχνίδι ισορροπίας:
Ο πρώτος αναδιατάσσει με τυχαίο τρόπο μεταξύ τους τα ταμπελάκια με τα γράμματα από το a έως το h. Στη συνέχεια αναδιατάσσει με τυχαίο τρόπο μεταξύ τους τα ταμπελάκια με τους αριθμούς από το 1 έως το 8.
Ο δεύτερος τοποθετεί τα 8 βαρίδια στη σκακιέρα έτσι ώστε να καλυφθούν τα τετράγωνα a1, b2, c3, d4, e5, f6, g7, h8. Οι συντεταγμένες που θα τοποθετήσει τα βαρίδια είναι όπως διαμορφώθηκαν μετά τις αλλαγές που έκανε ο πρώτος.
Ποια είναι η πιθανότητα στο τέλος αυτής της διαδικασίας, η σκακιέρα να συνεχίσει να ισορροπεί;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ας ονομάσουμε "νόμιμη" μία διάταξη των ακεραίων αριθμών από το 1 έως το 14, αν για κάθε αριθμό μ, όπου 1 < μ ≤ 14, το ακέραιο μέρος του μ/2 προηγείται του μ στη διάταξη. Ποια είναι η πιθανότητα μια τυχαία διάταξη των 14 αριθμών να είναι νόμιμη;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

50 μαθητές, διαφορετικών μεταξύ τους αναστημάτων, στοιχίζονται με τυχαίο τρόπο σε μία σειρά. Στη συνέχεια ο δάσκαλός τους, ξεκινώντας από τους δύο που βρίσκονται στις θέσεις 1-2, συγκρίνει τα αναστήματά τους και, αν χρειάζεται, αλλάζει τη μεταξύ τους θέση βάζοντας στη θέση 2 τον ψηλότερο και στη θέση 1 τον κοντύτερο μαθητή. Κατόπιν επαναλαμβάνει την ίδια διαδικασία με τους μαθητές που βρίσκονται τώρα στις θέσεις 2-3, μετά με τους μαθητές που βρίσκονται στις θέσεις 3-4 κ.ο.κ. και σταματάει αφού κάνει το ίδιο με τους μαθητές των θέσεων 49-50, βάζοντας πάντα στη μεγαλύτερης τάξης θέση τον ψηλότερο από τους δύο. Σε μία τυχαία αρχική διάταξη των μαθητών, ποια είναι η πιθανότητα ο μαθητής που βρίσκεται αρχικά στη θέση 7 να βρεθεί τελικά στη θέση 24;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ένα τραπέζι ορθογώνιου σχήματος στηρίζεται σε 4 πόδια, ένα σε κάθε γωνία του, που το καθένα έχει ένα τυχαίο ακέραιο μήκος από 91 έως 98 εκατοστά. Ποια είναι η πιθανότητα το τραπέζι να μην κουτσαίνει, δηλαδή οι απολήξεις των ποδιών του να είναι συνεπίπεδες;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Αν πάρουμε 4 τυχαία σημεία πάνω στην επιφάνεια μιας σφαίρας, ποια είναι η πιθανότητα το τετράεδρο που έχει για κορυφές αυτά τα 4 σημεία να περιέχει στο εσωτερικό του το κέντρο της σφαίρας;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ποια είναι η πιθανότητα να έχουν γεννηθεί 6 άνθρωποι μέσα σε οποιουσδήποτε δύο μήνες;
Διευκρίνιση: Θεωρήστε πως όλοι οι μήνες έχουν τις ίδιες μέρες.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Το μεσαίο διάζωμα ενός κινηματογράφου έχει 7 θέσεις σε κάθε σειρά, αριθμημένες με τους αριθμούς από 1 έως 7 και ο κάθε θεατής κάθεται στον αριθμό της θέσης που αναγράφεται στο εισιτήριό του. Σε μία από τις σειρές έχουν κοπεί όλα τα εισιτήρια και έχουν αγορασθεί από τους θεατές Α, Β, Γ, Δ, Ε, Ζ και Η, με τυχαία σειρά. Ο καθένας από αυτούς τους θεατές έχει έρθει μόνος του και όλοι έφτασαν αφού είχε αρχίσει η ταινία και με αλφαβητική σειρά, δηλαδή πρώτος έφτασε ο Α και τελευταίος ο Η.
Ποια είναι η πιθανότητα να κάτσει ο καθένας στη θέση του χωρίς να αναγκαστεί να περάσει μπροστά από κάποιον από τους υπολοίπους;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο τοπικός μετεωρολόγος προβλέπει ότι δεν θα βρέξει αύριο στο Πήλιο, ενώ αντίθετα η ΕΜΥ προβλέπει βροχή. Οι δύο πηγές είναι ανεξάρτητες και, βάσει ιστορικού, οι προβλέψεις του μεν μετεωρολόγου επιβεβαιώνονται στα 4/5 των περιπτώσεων, της δε ΕΜΥ στα 8/9 των περιπτώσεων. Χωρίς καμία άλλη πληροφορία, εσείς ποια νομίζετε ότι είναι η πιθανότητα να βρέξει αύριο στο Πήλιο;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Στο σχήμα βλέπετε τη σκιά ενός μπερδεμένου βραχιολιού με κούμπωμα. Ποια είναι η πιθανότητα εάν τεντώσουμε αυτό το βραχιόλι να δεθεί κόμπος;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο Άρης, ο Βασίλης, ο Γιάννης και ο Δημήτρης είναι τέσσερις φίλοι που ο καθένας τους λέει αλήθεια με πιθανότητα 1 στις 3 και ψέματα με πιθανότητα 2 στις 3.
Ο Άρης, ο Βασίλης και ο Γιάννης κάνουν με αυτή τη σειρά από μία δήλωση και στη συνέχεια ο Δημήτρης λέει ότι ο Γιάννης λέει ότι ο Βασίλης λέει ότι ο Άρης έλεγε την αλήθεια. Ποια είναι η πιθανότητα ο Άρης να έλεγε πράγματι την αλήθεια;

Διευκρινίσεις:
1. Ο καθένας τους γνωρίζει πότε ο άλλος λέει αλήθεια και πότε ψέματα.
2. Εμείς γνωρίζουμε μόνο τη δήλωση του Δημήτρη, αλλά ξέρουμε πως οι δηλώσεις του Βασίλη και του Γιάννη έχουν παρόμοια δομή.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο Mr. Riddler εξηγεί στους παίκτες Α και Β το παιχνίδι που πρόκειται να παίξουν: «Έχω στο γραφείο μου κάποιους φακέλους, ο καθένας από τους οποίους περιέχει ένα διαφορετικό χρηματικό ποσό. Θα διαλέξω στην τύχη έναν από αυτούς τους φακέλους, θα δω το ποσό που περιέχει και θα τον δώσω κλειστό στον παίκτη Α. Στη συνέχεια θα στρίψω ένα νόμισμα και αν φέρει Γράμματα θα βάλω σε έναν νέο φάκελο το μισό ποσό από αυτό που περιέχει ο φάκελος του παίκτη Α, ενώ αν φέρει Κορώνα θα βάλω μέσα το διπλάσιο ποσό. Αυτόν τον φάκελο θα τον δώσω κλειστό στον παίκτη Β. Στη συνέχεια θα σας καλέσω με τη σειρά στο γραφείο μου και θα σας ζητήσω να αποφασίσετε αν θέλετε να ανταλλάξετε φακέλους με τον άλλο παίκτη ή όχι. Αν ζητήσετε και οι δύο ανταλλαγή τότε αυτή θα πραγματοποιηθεί, αλλιώς θα μείνει ο καθένας με τον αρχικό του φάκελο. Το ποσό που θα καταλήξει στον καθένα σας θα είναι δικό σας».
Πράγματι ακολουθήθηκε αυτή η διαδικασία, αλλά πριν ο Mr. Riddler φωνάξει τον παίκτη Α στο γραφείο του, ο Α λέει στον Β ότι μιας και δεν τους βλέπει ο Riddler, δεν θα είχε αντίρρηση αν ο Β αποκάλυπτε το ποσό του φακέλου του ώστε να βοηθηθούν λίγο στην απόφασή τους. Ο Β συμφωνεί, ανοίγει τον φάκελό του και βλέπουν και οι δύο πως περιέχει το ποσό των 100 ευρώ. Στη συνέχεια ο Mr. Riddler καλεί τους δύο παίκτες με τη σειρά να του ανακοινώσουν την απόφασή τους.
Ποια απόφαση αποδίδει το μεγαλύτερο αναμενόμενο κέρδος ξεχωριστά για τους παίκτες Α και Β και γιατί;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Είναι γνωστό ότι το λεωφορείο μιας γραμμής φτάνει σε μια συγκεκριμένη στάση οποιαδήποτε στιγμή από τις 9:00 έως τις 9:30 και μετά δεν ξαναπερνά.
Ένας άνθρωπος καταφθάνει στην ίδια στάση μία τυχαία ώρα μεταξύ του παραπάνω διαστήματος. Υπολογίστε την πιθανότητα να πάρει το λεωφορείο μέσα στα επόμενα 5 λεπτά από τη στιγμή που θα φτάσει στη στάση.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο κυρ Τάσος πήγε για πρώτη φορά στη ζωή του στο καζίνο να δοκιμάσει την τύχη του. Είχε φέρει μαζί του 100 ευρώ που τα έδωσε στο ταμείο και πήρε 100 μάρκες. Είχε ακούσει πως η ρουλέτα είναι το πιο δίκαιο παιχνίδι για τους παίκτες, οπότε είπε να παίξει σ’ αυτήν. Ο τροχός της ρουλέτας έχει 37 νούμερα, εκ των οποίων τα 18 είναι κόκκινα, τα 18 μαύρα και ένα πράσινο, το μηδέν. Ήξερε πως αν ποντάρει μία μάρκα στο κόκκινο και η μπίλια κάτσει σε κόκκινο νούμερο τότε θα κέρδιζε άλλη μία μάρκα ενώ αν ερχόταν μαύρο νούμερο ή το μηδέν θα έχανε τη μάρκα που πόνταρε.
Είχε αποφασίσει εξ αρχής πως θα έπαιζε μέχρι να διπλασιάσει τις μάρκες του ή μέχρι να τις χάσει όλες. Αρχικά σκέφτηκε να ποντάρει και τις 100 μάρκες του στο κόκκινο, αλλά τότε το παιχνίδι του θα τελείωνε σε μόλις μία ριξιά της μπίλιας. Οπότε θέλησε να το κάνει λίγο πιο περιπετειώδες: Θα πόνταρε μία μάρκα κάθε φορά στο κόκκινο και μόλις συγκέντρωνε 200 μάρκες ή τις έχανε όλες θα έφευγε απ’ το καζίνο.
Ποια είναι η πιθανότητα να διπλασιάσει κάποια στιγμή ο κυρ Τάσος τις μάρκες του; Δεν ζητείται η ακριβής πιθανότητα, μόνο σε ποιο από τα παρακάτω διαστήματα βρίσκεται:
Α. [0% έως 1%)       Β. [1% έως 10%)       Γ. [10% έως 50%)       Δ. Ακριβώς 50%       Ε. (50% έως 90%]       ΣΤ. (90% έως 99%]       Ζ. (99% έως 100%]

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ένα βακτήριο έχει πιθανότητα 80% να διαιρεθεί και να σχηματίσει δύο βακτήρια και πιθανότητα 20% να μη διαιρεθεί και να πεθάνει. Το ίδιο ισχύει και για τους πιθανούς απογόνους του.
Ξεκινώντας από ένα βακτήριο, ποια είναι ακριβής πιθανότητα να επιβιώσει η αποικία για πάντα;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Παίρνουμε ένα μακρύ σπίρτο (από αυτά που ανάβουμε το τζάκι) και σημειώνουμε πάνω του δύο τυχαία σημεία. Στη συνέχεια σπάμε το σπίρτο στα σημεία αυτά και μένουμε με τρία κομμάτια του σπίρτου.
Ποια είναι η πιθανότητα να μπορούν να ενωθούν αυτά τα τρία κομμάτια ώστε να σχηματίζουν ένα τρίγωνο;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έχουμε μία στάμνα που περιέχει ανακατεμένους 49 λευκούς και 51 μαύρους βόλους. Οι βόλοι διαφέρουν μεταξύ τους μόνο ως προς το χρώμα τους.
Πόσους βόλους πρέπει να τραβήξουμε με κλειστά τα μάτια, ώστε να μεγιστοποιήσουμε την πιθανότητα να βγάλουμε ίσο αριθμό λευκών και μαύρων βόλων;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έχουμε μία τράπουλα με 52 φύλλα στην οποία προσθέτουμε και τον έναν τζόκερ. Ανακατεύουμε τα 53 φύλλα και τα απλώνουμε κλειστά πάνω σε ένα τραπέζι. Ανοίγουμε ένα-ένα τα φύλλα με τυχαία σειρά.
Ποια είναι η πιθανότητα όταν θα ανοίξουμε τον τζόκερ να έχουμε ανοίξει ήδη τους τέσσερις άσσους της τράπουλας;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Σε μια πόλη της Άγριας Δύσης έπιασαν έναν ξένο που έκλεβε στα χαρτιά. Μιας και ήταν τζογαδόρος, ο σερίφης αποφάσισε η μοίρα του να κριθεί στην τύχη.
Έβαλε λοιπόν δύο σφαίρες σε ένα εξάσφαιρο πιστόλι με μύλο και αποφάσισε να πατήσει τη σκανδάλη δύο φορές με το όπλο στραμμένο προς τον κλέφτη. Αν και τις δύο φορές το όπλο δεν πυροβολούσε, τότε θα του χαριζόταν η ζωή. Για να μην κατηγορηθεί μάλιστα για μεροληψία, ο σερίφης γύρισε δυνατά τον μύλο πριν τον κλείσει ώστε να μη γνωρίζει ούτε ο ίδιος τη θέση των δύο σφαιρών πριν πατήσει τη σκανδάλη.
Πατάει λοιπόν τη σκανδάλη για πρώτη φορά και το όπλο κάνει «κλικ», χωρίς να πυροβολήσει. Στο σημείο αυτό ο σερίφης ρωτάει τον κλέφτη αν προτιμάει να ξαναγυρίσει τυχαία τον μύλο πριν πατήσει τη σκανδάλη για δεύτερη φορά ή να πατήσει τη σκανδάλη με τη θαλάμη που είναι οπλισμένη εκείνη τη στιγμή, δηλαδή στην αμέσως επόμενη θέση από την πρώτη απόπειρα.
Ο κλέφτης, σαν τζογαδόρος που ήταν, γνώριζε από πιθανότητες, γι αυτό ρώτησε τον σερίφη αν τοποθέτησε τις σφαίρες στο πιστόλι τη μία δίπλα στην άλλη ή όχι.
Ανάλογα με την απάντηση του σερίφη ξέρει τι θα ζητήσει να γίνει με τον μύλο ώστε να μεγιστοποιήσει την πιθανότητά του να του χαριστεί η ζωή.
Ποια θα είναι η απόφασή του για κάθε μία από τις ακόλουθες πιθανές απαντήσεις του σερίφη;

Α) «Έβαλα τις σφαίρες σε διαδοχικές θέσεις»
Β) «Δεν έβαλα τις σφαίρες σε διαδοχικές θέσεις»
Γ) «Πολλά ρωτάς. Πάρε μια απόφαση τώρα!»

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ