Πιο γρήγορο τρένο (***)
Δύο τρένα ξεκινούν την ίδια στιγμή, το ένα από Αθήνα προς Θεσσαλονίκη και το άλλο από Θεσσαλονίκη προς Αθήνα και κινούνται με σταθερή ταχύτητα. Αφότου πέρασαν το ένα μπροστά από το άλλο, το πρώτο φτάνει στον προορισμό του 1 ώρα μετά και το άλλο φτάνει στον προορισμό του 4 ώρες μετά. Πόσες φορές ταχύτερο είναι το ένα τρένο από το άλλο;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Σκύλος με τενεκεδάκι (***)
Ένας σκύλος τρέχει από την Αθήνα στη Θεσσαλονίκη. Η απόσταση των δύο πόλεων είναι 500 χιλιόμετρα. Στην ουρά του έχει κρεμασμένο ένα τενεκεδάκι. Με αρχική ταχύτητα 1 μέτρο το δευτερόλεπτο, κάνει βήματα του ενός μέτρου και σε κάθε βήμα το τενεκεδάκι χτυπάει στο έδαφος. Κάθε φορά που ακούει τον χτύπο, τρομάζει και διπλασιάζει την ταχύτητά του. Με τι ταχύτητα θα φτάσει στη Θεσσαλονίκη;
Υπόδειξη: Ο γρίφος χρειάζεται λίγη Φυσική εκτός από Μαθηματικά. Θεωρήστε πως ο σκύλος είναι ικανός να πιάσει τις ταχύτητες που απαιτεί το πρόβλημα.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Μολύβι, στυλό, τετράδιο (****)
Ένα μολύβι, ένα στυλό και ένα τετράδιο κοστίζουν μαζί 1 ευρώ. Το τετράδιο κοστίζει περισσότερο από 2 μολύβια. 3 μολύβια κοστίζουν περισσότερο από 4 στυλό. 3 στυλό κοστίζουν περισσότερο από ένα τετράδιο. Πόσο κοστίζει το καθένα;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Arrival (****)
Δύο εξωγήινοι επισκέπτονται τη Γη. Για να τσεκάρουν την ευφυΐα των Γήινων, μας βάζουν τον παρακάτω γρίφο στη γλώσσα μας, ώστε να μπορούμε να τους καταλάβουμε: «Γεια σας Γήινοι! Ονομάζομαι Sloezzuar και είμαι 31 ετών. Ο συνάδελφός μου ο Gravrehz είναι 26 ετών. Το άθροισμα των ηλικιών μας είναι 60 έτη. Πόσα πλοκάμια έχουμε;»
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Ο τελευταίος επιζών (***)
Ένας πληρωμένος δολοφόνος έχει βρει απασχόληση σε μία πόλη όπου όλοι οι κάτοικοι μισιούνται μεταξύ τους. Η πόλη αποτελείται από 3000 σπίτια τοποθετημένα σε κυκλική διάταξη και σε κάθε σπίτι ζει ένας κάτοικος. Ο κάτοικος του σπιτιού 1 πληρώνει τον δολοφόνο για να δολοφονήσει τον πλησιέστερο γείτονα στα αριστερά του, δηλαδή τον κάτοικο του σπιτιού 2. Ο δολοφόνος εκτελεί το συμβόλαιο και στη συνέχεια επισκέπτεται τον πλησιέστερο κάτοικο προς τα αριστερά, δηλαδή τον κάτοικο του σπιτιού 3 και πληρώνεται από αυτόν για να δολοφονήσει τον πλησιέστερο γείτονά του, πάντα προς τα αριστερά. Η διαδικασία επαναλαμβάνεται μέχρι να μείνει μόνο ένας κάτοικος στην πόλη. Ποιος θα είναι ο αριθμός σπιτιού του τελευταίου επιζώντα;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Ανώμαλη διαδρομή (***)
Ένας ποδηλάτης ξεκινάει από την πόλη Α και κινείται στις κατηφόρες με ταχύτητα 36 χλμ/ω (χιλιόμετρα την ώρα), στον ίσιο δρόμο με ταχύτητα 31,5 χλμ/ω και στις ανηφόρες με ταχύτητα 28 χλμ/ω. Μετά από 4 ώρες φτάνει στην πόλη Β. Για το ταξίδι της επιστροφής χρειάστηκε 4 ώρες και 40 λεπτά. Πόση είναι η απόσταση μεταξύ των δύο πόλεων;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Εξίσωση με ακέραιες λύσεις (***)
Ο καθηγητής γράφει στον πίνακα την εξίσωση: x2 + 8x + 14 = 0
Σηκώνει κάθε φορά έναν μαθητή στον πίνακα και του λέει να αλλάζει κατά μία ακέραια μονάδα είτε το συντελεστή του x είτε το σταθερό όρο. Μετά από αρκετές επαναλήψεις της διαδικασίας, προέκυψε στον πίνακα η εξίσωση: x2 + 17x + 9 = 0
Να αποδειχθεί ότι μεταξύ της αρχικής και της τελικής εξίσωσης προέκυψε στον πίνακα εξίσωση που είχε ακέραιες λύσεις.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Αυτοκόλλητα (***)
Ένας μικρός άρχισε να μαζεύει αυτοκόλλητα χαρτάκια ποδοσφαίρου της Panini. Το άλμπουμ που τα κολλάει έχει 384 αριθμημένες θέσεις. Τα αυτοκόλλητα είναι επίσης αριθμημένα και το καθένα αντιστοιχεί σε μία θέση του άλμπουμ. Πωλούνται σε κλειστά φακελάκια και η τιμή του κάθε αυτοκόλλητου είναι 0,12 ευρώ.
Ο πατέρας του θέλει να υπολογίσει πόσο θα του στοιχίσει μέχρι να συμπληρώσει ο μικρός όλο το άλμπουμ. Υπέθεσε πως σε κάθε αγορά υπάρχει ίση πιθανότητα να αποκτηθεί οποιοδήποτε από τα 384 αυτοκόλλητα και πως ο μόνος τρόπος απόκτησης αυτοκόλλητων είναι η αγορά τους επιλέγοντας τυχαία κλειστά φακελάκια. Ποιο είναι το μέσο κόστος για τη συμπλήρωση του άλμπουμ;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Πακέτα κοτόπουλο (***)
Ένα φαστφουντάδικο πουλάει τηγανητό κοτόπουλο σε μικρά πακέτα των 6 κομματιών, μεσαία πακέτα των 9 κομματιών και μεγάλα πακέτα των 20 κομματιών. Ποιος είναι ο μεγαλύτερος αριθμός κομματιών που δεν μπορεί να παραγγελθεί;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Κατσίκια, χοίροι και πρόβατα (***)
Ένας κτηνοτρόφος έχει κατσίκια, χοίρους και πρόβατα. Το πλήθος του κάθε είδους είναι ένας διαφορετικός πρώτος αριθμός. Κάνοντας κάποιους υπολογισμούς διαπίστωσε ότι το γινόμενο του αριθμού των κατσικιών με το άθροισμα των αριθμών κατσικιών και χοίρων ήταν κατά 120 μεγαλύτερο από τον αριθμό των προβάτων. Πόσα ζώα έχει;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Χωνάκι παγωτό (***)
Ένας μικρός θέλει να αγοράσει ένα χωνάκι με όσο το δυνατόν μεγαλύτερη μπάλα παγωτό πάνω του. Πρέπει όμως τουλάχιστον η μισή μπάλα να βρίσκεται μέσα στο χωνάκι για να μην του πέσει. Το χωνάκι είναι ένας κώνος με ύψος 10 εκατοστά και ακτίνα κύκλου στο χείλος του 5 εκατοστά. Ποια είναι η ακτίνα της μεγαλύτερης δυνατής μπάλας παγωτό που μπορεί να χωρέσει μέσα;
Διευκρίνιση: Η μπάλα δεν πρέπει να πιεστεί και να αλλάξει σχήμα μέσα στο χωνάκι.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Εξερευνώντας τον κύβο (****)
Ένα ζωύφιο ξεκινάει από μια κορυφή ενός κύβου ζάχαρης με μήκος ακμής 1 εκατοστό και κινείται πάνω στις ακμές του κύβου. Σε κάθε κορυφή που φτάνει υπάρχει ίση πιθανότητα να διαλέξει οποιαδήποτε από τις 3 δυνατές κατευθύνσεις. Πόση απόσταση θα χρειαστεί να καλύψει κατά μέσο όρο προκειμένου να φτάσει στη διαγωνίως απέναντι κορυφή του κύβου;
Διευκρίνιση: Η ελάχιστη απόσταση για να φτάσει στη ζητούμενη κορυφή είναι 3 εκατοστά.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Ποδήλατο και πατίνι (****)
Τρεις φίλοι ξεκινούν από την πόλη Α και θέλουν να φτάσουν στην πόλη Β, όσο τον δυνατόν πιο γρήγορα. Η απόσταση των δύο πόλεων είναι 30 χιλιόμετρα. Έχουν στη διάθεσή τους ένα ποδήλατο που κινείται με ταχύτητα έως και 30 χιλιόμετρα την ώρα και ένα πατίνι που κινείται με ταχύτητα έως και 20 χιλιόμετρα την ώρα. Μπορούν όμως και να τρέχουν με τα πόδια με ταχύτητα έως και 10 χιλιόμετρα την ώρα.
Αν το επιθυμούν, μπορούν να αφήνουν το ποδήλατο και το πατίνι στην άκρη του δρόμου ώστε να το πάρει κάποιος άλλος που έρχεται από πίσω. Ποιος είναι ο ελάχιστος χρόνος που θα χρειαστούν για να φτάσουν και οι τρεις στην πόλη Β και με ποιον τρόπο θα τα καταφέρουν;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Πρωτοφανείς αριθμοί (****)
Ονομάζουμε έναν φυσικό αριθμό "πρωτοφανή" αν είναι σύνθετος, αλλά όχι πολλαπλάσιος του 2 ή του 3 ή του 5. Πόσοι πρωτοφανείς είναι μικρότεροι του 10.000;
Σημείωση: Υπάρχουν 1229 πρώτοι αριθμοί μέχρι το 10.000.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
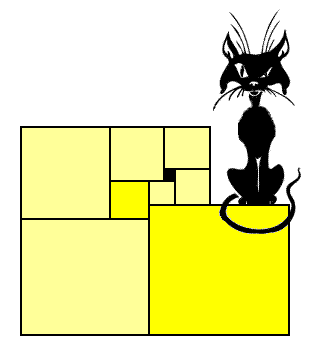
Σωρός από κιβώτια (***)

Όλες οι έδρες των κιβωτίων που φαίνονται στο σχήμα είναι τετράγωνα. Το μικρό μαύρο κενό που έχει δημιουργηθεί ανάμεσά τους είναι κι αυτό τετράγωνο με μήκος πλευράς 1 εκατοστό. Πόσο είναι το μήκος των πλευρών του κιβωτίου πάνω στο οποία κάθεται ο γάτος;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Συζυγία δεικτών του ρολογιού (***)
Βρείτε την ώρα που συναντώνται για πρώτη φορά μετά τις 12, ο ωροδείκτης και ο λεπτοδείκτης ενός ρολογιού, με ακρίβεια δευτερολέπτου.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Διπλάσιο – τριπλάσιο – πενταπλάσιο (****)
Βρείτε τον μικρότερο θετικό ακέραιο αριθμό του οποίου το διπλάσιο είναι τέλειο τετράγωνο, το τριπλάσιο είναι τέλειος κύβος και το πενταπλάσιο είναι τέλεια 5η δύναμη.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Το πέρασμα του ποταμού (****)
Ο Νίκος ξεκίνησε από τη Νικόπολη στις 10:18 π.μ. και περπατώντας με σταθερή ταχύτητα έφτασε στην Γεωργιούπολη στις 1:30 μ.μ.
Την ίδια ημέρα, ο Γιώργος ξεκίνησε από την Γεωργιούπολη στις 9:00 π.μ. και περπατώντας με σταθερή ταχύτητα στον ίδιο δρόμο έφτασε στη Νικόπολη στις 11:40 π.μ.
Αυτός ο δρόμος περνάει πάνω από ένα πλατύ ποτάμι με μία γέφυρα. Ο Νίκος και ο Γιώργος έφτασαν ταυτόχρονα στο ποτάμι, ο καθένας από τη δική του πλευρά της όχθης. Ο Νίκος κατέβηκε από τη γέφυρα 1 λεπτό αργότερα από τον Γιώργο.
Τι ώρα έφτασαν στο ποτάμι;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Λάθος στην επιταγή (***)
Χτες πήγα στη τράπεζα να εξαργυρώσω μια επιταγή. Ο ταμίας μου έδωσε τα χρήματα και τα έβαλα στην τσέπη μου χωρίς να τα μετρήσω. Εκείνη την ημέρα ξόδεψα 6,23 ευρώ. Το βράδυ, όταν μέτρησα τα χρήματα που είχαν απομείνει στην τσέπη μου, ανακάλυψα ότι, παραδόξως, ήταν διπλάσια από το ποσό της επιταγής που είχα δώσει στην τράπεζα. Έπειτα κατάλαβα πως ο ταμίας είχε κατά λάθος αντιστρέψει τον αριθμό των ευρώ με τον αριθμό των λεπτών της επιταγής στα χρήματα που μου έδωσε. Ποιο ήταν το ποσό της επιταγής;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Διπλάσιο και μισό (****)
Βρείτε ένα φυσικό αριθμό για τον οποίο αν πάρουμε το πρώτο ψηφίο του και το τοποθετήσουμε τελευταίο, ο αριθμός που θα προκύψει θα είναι ο μισός του αρχικού.
Παράδειγμα: Το 321 γίνεται 213, αλλά το 213 δεν είναι το μισό του 321.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Κούρεμα γκαζόν (***)
Τρεις κηπουροί, ο Αποστόλης, ο Βαγγέλης και ο Γιάννης, κουρεύουν κάθε μήνα το γκαζόν ενός μεγάλου κήπου. Αν το κούρευε μόνος του ο Αποστόλης θα έκανε 1 ώρα παραπάνω απ’ ότι κάνουν και οι τρεις μαζί. Αν το κούρευε μόνος του ο Βαγγέλης θα έκανε 5 ώρες παραπάνω και αν το κούρευε μόνος του ο Γιάννης θα έκανε 8 ώρες παραπάνω.
Σε πόση ώρα κουρεύουν το γκαζόν ο Αποστόλης και ο Βαγγέλης μαζί;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Στο δρόμο για τη Μέκκα (***)
Δύο Άραβες φίλοι κατευθύνονται προς τη Μέκκα για να προσκυνήσουν. Στο δρόμο σταματούν να ξεκουραστούν και να φάνε. Βγάζει ο πρώτος από το σάκο του 4 καρβέλια ψωμί και ο δεύτερος 7 καρβέλια ψωμί. Εκείνη τη στιγμή, τους πλησιάζει ένας τρίτος προσκυνητής και τους λέει πως πεινάει αλλά δεν έχει μαζί του καθόλου φαγητό. Τους παρακαλεί να του δώσουν από το δικό τους και να το πληρώσει. Οι δύο φίλοι δέχονται αμέσως να μοιραστούν τα καρβέλια τους ώστε να φάνε και οι τρεις την ίδια ποσότητα.
Αφού έφαγαν όλα τα καρβέλια, ο ξένος τους ευχαριστεί πολύ και τους αφήνει 22 φλουριά που είχε μαζί του σαν αντάλλαγμα για το ψωμί που του έδωσαν. Ποιος είναι ο πιο δίκαιος τρόπος για να μοιραστούν οι δύο φίλοι τα φλουριά;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Τα τέσσερα ρομπότ (****)
Τέσσερα ρομπότ βρίσκονται στις θέσεις Α,Β,Γ,Δ σχηματίζοντας ένα τετράγωνο, όπως φαίνεται στο σχήμα.
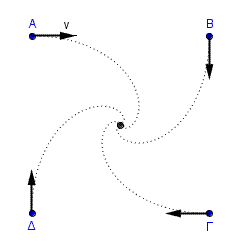
Ξεκινούν να κινούνται όλα ταυτόχρονα με ταχύτητα σταθερού μέτρου ν και το καθένα με διεύθυνση προς την τρέχουσα θέση του ενός διπλανού του. Τελικά όλα τα ρομπότ θα συναντηθούν στο κέντρο του τετραγώνου διαγράφοντας μία καμπύλη διαδρομή.
Αν L είναι η αρχική απόσταση μεταξύ δύο διαδοχικών ρομπότ, υπολογίστε τον χρόνο t που θα περάσει μέχρι να συναντηθούν.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Τέλεια τετράγωνα (***)
Ξεκινάμε από έναν ακέραιο αριθμό α. Αν του προσθέσουμε 30 τότε το αποτέλεσμα είναι ένα τέλειο τετράγωνο. Αν του αφαιρέσουμε 30 τότε το αποτέλεσμα είναι επίσης ένα τέλειο τετράγωνο. Πόσοι τέτοιοι αριθμοί α υπάρχουν;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Αυξανόμενο υπόλοιπο (***)
Ποιος είναι ο μικρότερος αριθμός που συγκεντρώνει όλες τις παρακάτω ιδιότητες;
Όταν διαιρεθεί με το 2 να αφήνει υπόλοιπο 1
Όταν διαιρεθεί με το 3 να αφήνει υπόλοιπο 2
Όταν διαιρεθεί με το 4 να αφήνει υπόλοιπο 3
Όταν διαιρεθεί με το 5 να αφήνει υπόλοιπο 4
Όταν διαιρεθεί με το 6 να αφήνει υπόλοιπο 5
Όταν διαιρεθεί με το 7 να αφήνει υπόλοιπο 6
Όταν διαιρεθεί με το 8 να αφήνει υπόλοιπο 7
Όταν διαιρεθεί με το 9 να αφήνει υπόλοιπο 8
Όταν διαιρεθεί με το 10 να αφήνει υπόλοιπο 9
Σωστές θα θεωρούνται οι απαντήσεις που περιγράφουν τη λογική διαδικασία που οδηγεί στο αποτέλεσμα, χωρίς να κάνουν καμία χρήση δοκιμαστικών διαιρέσεων.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Το κυνήγι της χήνας (****)
Μια χήνα βρίσκεται στο κέντρο μιας κυκλικής λίμνης. Ένας λύκος βρίσκεται στην όχθη της λίμνης και θα ήθελε πολύ να τη φάει αλλά δεν ξέρει κολύμπι. Αν η χήνα καταφέρει να κολυμπήσει μέχρι την όχθη της λίμνης τότε μπορεί στιγμιαία να πετάξει και να γλυτώσει από τα δόντια του λύκου. Ο λύκος τρέχει 4 φορές πιο γρήγορα απ’ ότι κολυμπάει η χήνα και κινείται πάντοτε προς την κατεύθυνση που τον φέρνει πιο κοντά της.
Μπορεί να γλυτώσει η χήνα; Αν ναι, περιγράψτε τη διαδρομή που πρέπει να ακολουθήσει και δώστε μια εκτίμηση του ελάχιστου μήκους της.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Το ρολόι της Τικ-τοκ (*****)
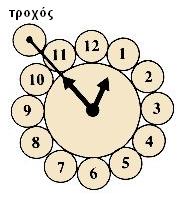
Η πόλη Τικ-τοκ έχει ένα ρολόι που μένει για πάντα στη μνήμη όσων την επισκέπτονται. Όπως φαίνεται και στο σχήμα, το ρολόι αποτελείται από 12 όμοιους αριθμημένους δίσκους, τοποθετημένους σε κύκλο έτσι ώστε ο κάθε δίσκος να εφάπτεται με τους δύο γειτονικούς του και με τον μεγάλο κυκλικό δίσκο στο κέντρο. Το ρολόι έχει επίσης στην εξωτερική πλευρά του έναν τροχό, που έχει την ίδια ακτίνα με τους 12 δίσκους και συνδέεται από το κέντρο του στον λεπτοδείκτη του ρολογιού με μία βέργα και ένα ελατήριο. Το ελατήριο τραβάει τον τροχό προς το κέντρο του ρολογιού, έτσι ώστε καθώς ο λεπτοδείκτης περιστρέφεται, ο τροχός να κυλάει πάνω στους δίσκους χωρίς να χάνει ποτέ την επαφή του με αυτούς.
Ένα μυρμήγκι έχει ανέβει πάνω στον λεπτοδείκτη και κοιτάζει τον εξωτερικό τροχό. Πόσες φορές θα τον δει να περιστρέφεται σε διάστημα μίας ώρας;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Δεκαδικός ως κλάσμα δύο ακεραίων (****)
Βρείτε δύο ακέραιους αριθμούς, οι οποίοι όταν διαιρεθούν ο ένας με τον άλλον το αποτέλεσμα να είναι ο αριθμός 0,35624624624… με την ακολουθία 624 να επαναλαμβάνεται επ’ άπειρον.
Υπόδειξη: Δεν ενδείκνυται να βρείτε τους δύο ακεραίους με δοκιμές γιατί είναι σχετικά μεγάλοι αριθμοί. Θα πρέπει να ανακαλύψετε έναν μηχανισμό που να δίνει με αλγεβρικό τρόπο το ζητούμενο αποτέλεσμα. Άπαξ και τον βρείτε, μπορεί να χρησιμοποιηθεί για την εύρεση οποιουδήποτε άλλου δεκαδικού αριθμού με περιοδικά ψηφία. Ο συγκεκριμένος δεκαδικός του προβλήματος δεν έχει κάτι το ιδιαίτερο και δίνεται μόνο σαν παράδειγμα εφαρμογής του ζητούμενου μηχανισμού.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Στρατός μυρμηγκιών (***)
Ένας στρατός μυρμηγκιών έχει παραταχθεί σε μία γραμμή μήκους ενός μέτρου, ο ένας πίσω από τον άλλον και κινούνται με σταθερή ταχύτητα 6 μέτρα την ώρα. Ξαφνικά, το μυρμηγκάκι που βρίσκεται στο τέλος της ουράς θέλει να μεταδώσει ένα μήνυμα στον αρχηγό που βρίσκεται στην αρχή της ουράς. Ανοίγει λοιπόν το βήμα του, φτάνει στον αρχηγό με το μήνυμα και αμέσως επιστρέφει πάλι πίσω στη θέση του. Αυτή η αποστολή του μυρμηγκιού έγινε επίσης με σταθερή ταχύτητα και μόλις ολοκληρώθηκε, η γραμμή των μυρμηγκιών είχε μετακινηθεί κατά ένα μέτρο.
Ποια ήταν η ταχύτητα του μυρμηγκιού κατά τη διάρκεια της αποστολής του;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Γέμισμα μπανιέρας (**)
Μία μπανιέρα έχει από πάνω της τρεις βρύσες, με διαφορετική ροή η κάθε μία, συνδεδεμένες σε διαφορετικούς σωλήνες παροχής νερού. Η πρώτη βρύση, αν ανοιχτεί μόνη της, γεμίζει την μπανιέρα σε 3 ώρες, η δεύτερη γεμίζει την μπανιέρα σε 4 ώρες και η τρίτη σε 6 ώρες.
Σε πόσο χρόνο θα γεμίσει η μπανιέρα αν ανοιχτούν και οι τρεις βρύσες ταυτόχρονα;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Περίμετρος σχήματος (***)
Βρείτε την περίμετρο του παρακάτω σχήματος.
Τα στοιχεία που έχετε είναι τα τρία μήκη πλευρών που απεικονίζονται και πως όλες οι γωνίες τους σχήματος είναι ορθές.
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ
Διάσωση ναυαγών (**)
15 ναυαγοί βρίσκονται πάνω σε ένα πλοίο που πρόκειται να βουλιάξει σε 20 λεπτά. Αν οι ναυαγοί πέσουν στο νερό θα φαγωθούν από τους καρχαρίες που υπάρχουν τριγύρω. Ευτυχώς έχουν στη διάθεσή τους μία βάρκα με δύο κουπιά που χωράει όμως μέχρι 5 άτομα. Υπάρχει κοντά στο πλοίο ένα νησί που θα προσφέρει σωτηρία στους ναυαγούς που θα φτάσουν σε αυτό με τη βάρκα. Ο συνολικός χρόνος που χρειάζεται η βάρκα για να πάει στο νησί και να γυρίσει πίσω στο πλοίο είναι 9 λεπτά. Πόσοι ναυαγοί θα καταφέρουν να σωθούν;
Μόνο για Μέλη: στείλτε την απάντησή σας εδώ