Γρίφοι με Παράδοξα

Οι μη παράλληλες ευθείες δεν τέμνονται (****)

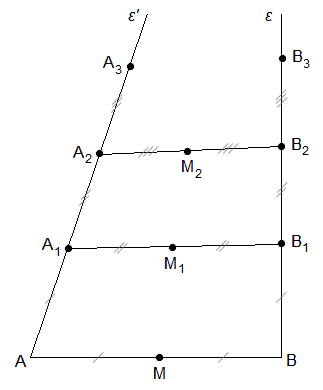
Στα άκρα ενός ευθύγραμμου τμήματος ΑΒ φέρνουμε μια κάθετη ευθεία ε και μία ευθεία ε' με μικρή κλίση προς τα δεξιά. Έστω Μ το μέσο του τμήματος ΑΒ. Πάνω στην ευθεία ε' παίρνουμε το σημείο Α₁ έτσι ώστε ΑΜ=ΑΑ₁ και πάνω στην ευθεία ε παίρνουμε το σημείο Β₁ έτσι ώστε ΒΜ=ΒΒ₁.
Ας αποδείξουμε ότι ευθείες ε και ε' δεν μπορεί να τέμνονται εντός των τμημάτων ΑΑ₁ και ΒΒ₁: Αν οι δύο ευθείες τέμνονται σε κάποιο σημείο Τ εντός των τμημάτων ΑΑ₁ και ΒΒ₁ θα έπρεπε να ισχύει ότι ΑΤ<ΑΑ₁ και ΒΤ<ΒΒ₁, άρα και ότι ΑΤ+ΤΒ < ΑΑ₁+ΒΒ₁. Όμως ΑΑ₁+ΒΒ₁ = ΑΒ, άρα θα ίσχυε ότι ΑΤ+ΤΒ < ΑΒ. Όμως στο τρίγωνο ΑΤΒ, το άθροισμα των δύο πλευρών του είναι πάντοτε μεγαλύτερο από την τρίτη πλευρά, οπότε καταλήξαμε σε αντίφαση. Άρα πράγματι οι δύο ευθείες δεν μπορεί να τέμνονται εντός των τμημάτων ΑΑ₁ και ΒΒ₁.
Φέρνουμε τώρα το ευθύγραμμο τμήμα Α₁Β₁, το μέσο του Μ₁ και τα σημεία Α₂ και Β₂ έτσι ώστε Α₁Μ₁=Α₁Α₂ και Β₁Μ₁=Β₁Β₂. Ακολουθώντας την προηγούμενη απόδειξη βρίσκουμε πως οι δύο ευθείες δεν μπορούν να τέμνονται εντός των τμημάτων Α₁Α₂ και Β₁Β₂.
Αυτή τη διαδικασία μπορούμε να την επαναλαμβάνουμε επ' άπειρον και να καταλήξουμε στο συμπέρασμα ότι οι ευθείες ε και ε' δεν τέμνονται πουθενά. Πού βρίσκεται το λάθος;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

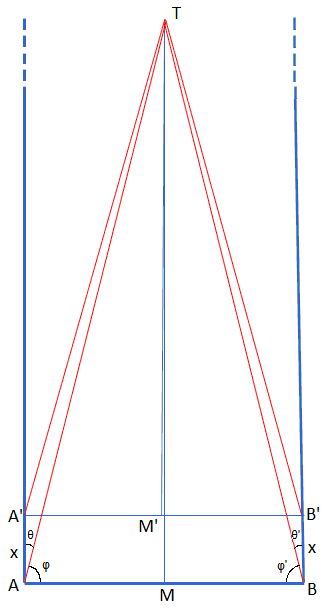
1. Έστω πως έχουμε ένα ευθύγραμμο τμήμα ΑΒ. Στο σημείο Α φέρνουμε μια κάθετη ημιευθεία. Στο σημείο Β, φέρνουμε μια σχεδόν κάθετη ημιευθεία, αλλά με πολύ μικρή κλίση προς τα αριστερά, όπως στο σχήμα. Προφανώς οι δυο ημιευθείες κάπου θα τέμνονται και θα σχηματίζεται ένα τρίγωνο. Το σημείο τομής τους δεν απεικονίζεται στο σχήμα.
2. Από το σημείο Α, φέρνουμε πάνω στην κάθετη πλευρά, μικρό τμήμα ΑΑ' μήκους x . Το ίδιο κάνουμε και στη σχεδόν κάθετη πλευρά με το τμήμα ΒΒ'.
3. Φέρνουμε τις μεσοκαθέτους στα μέσα Μ και Μ' των ΑΒ και Α'Β' αντίστοιχα. Αυτές επίσης θα τέμνονται σε ένα σημείο Τ.
4. Τα τρίγωνα ΑΤΒ και Α'ΤΒ' είναι ισοσκελή εκ κατασκευής και άρα οι γωνίες φ και φ' είναι ίσες.
5. Τα τρίγωνα Α'ΤΑ και ΒΤΒ' είναι ίσα, καθώς έχουν και τις τρεις πλευρές τους ίσες. Άρα οι γωνίες θ και θ' είναι ίσες.
6. Όμως φ + θ = 90 μοίρες, άρα και φ' + θ' = 90 μοίρες.
7. Συνεπώς το αρχικό μας τρίγωνο έχει δύο ορθές γωνίες!

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

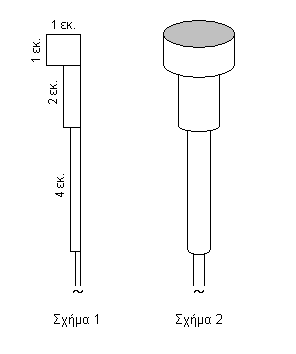
Στο Σχήμα 1 βλέπουμε μια επίπεδη επιφάνεια, χωρισμένη σε τμήματα. Το πρώτο τμήμα είναι τετράγωνο πλευράς $1\,εκ.$ Από το δεύτερο τμήμα και μετά, το κάθε νέο τμήμα έχει το διπλάσιο ύψος και το μισό πλάτος του προηγούμενου. Έτσι το εμβαδόν του κάθε τμήματος είναι πάντοτε $1\,εκ.^2$. Τα τμήματα αυτά είναι άπειρα σε πλήθος, οπότε το συνολικό τους εμβαδό είναι:
$E = 1\,εκ.^2 + 1\,εκ.^2 + 1\,εκ.^2 +\ldots$ , δηλαδή άπειρο.
Ένας μπογιατζής σκέφτεται πως αν ήθελε να βάψει αυτή την επιφάνεια θα χρειαζόταν άπειρη ποσότητα χρώματος.
Περιστρέφουμε τώρα την επιφάνεια γύρω από την ημιευθεία που βρίσκεται στο δεξιό σύνορο του Σχήματος 1 μέχρι να σχηματιστεί ένας πλήρης κύκλος. Προκύπτει έτσι το στερεό του Σχήματος 2 που αποτελείται από άπειρο πλήθος κυλίνδρων.
Ο όγκος ενός κυλίνδρου ακτίνας $r$ και ύψους $h$, δίνεται από τον τύπο: $V=πr^2h$.
O $ν\,$–οστός κύλινδρος του Σχήματος 2 μετρώντας από επάνω έχει ακτίνα $r=1/2^{ν-1}\,εκ.$ και ύψος $h=2^{ν-1}\,εκ.$ Άρα ο όγκος του $ν\,$–οστού κυλίνδρου είναι $V_ν=π/2^{ν-1}\,εκ.^3$.
Ο συνολικός όγκος του στερεού του σχήματος 2 είναι:
$$V=π\,(1+1/2+1/2^2+1/2^3+\ldots)\,εκ.^3$$ Μέσα στην παρένθεση του πιο πάνω τύπου έχουμε ένα γνωστό άθροισμα μιας γεωμετρική προόδου απείρων όρων, το οποίο συγκλίνει στην τιμή $2$. Άρα ο συνολικός όγκος του Σχήματος 2 είναι:
$$V=2π\,εκ.^3$$ Ας φανταστούμε τώρα ότι το στερεό του Σχήματος 2 είναι μέσα κούφιο, σχηματίζοντας ένα δοχείο. Για να το γεμίσει ο μπογιατζής θα χρειαζόταν χρώμα όγκου $2π\,εκ.^3$. Στη συνέχεια σκέφτεται πως εάν βουτούσε το επίπεδο του Σχήματος 1 μέσα στο δοχείο με το χρώμα, τότε θα το έβγαζε βαμμένο και μάλιστα και από τις δύο πλευρές.
Οδηγείται λοιπόν σε δύο αντιφατικά συμπεράσματα: το πρώτο είναι ότι το επίπεδο χρειάζεται άπειρη ποσότητα χρώματος για να βαφτεί και το δεύτερο είναι ότι αρκούν $6,28\,εκ.^3$ χρώματος περίπου. Σε ποιο σημείο του συλλογισμού του μπογιατζή βρίσκεται το λάθος;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Κατά τη γνώμη μου, όποιος επιλύει αυτό το παράδοξο χωρίς εξωτερική βοήθεια είναι ένας νέος Ισαάκ Νεύτων!
Για την παρακολούθηση της πιο κάτω απόδειξης απαιτούνται κάπως πιο προχωρημένες γνώσεις Φυσικής.
Μία σανίδα μήκους $L=1$ μέτρο, είναι γερμένη πάνω σε έναν τοίχο κάθετο με το έδαφος, όπως φαίνεται στο σχήμα.

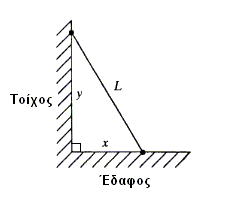
Πιάνουμε τη σανίδα από το κάτω άκρο της και την τραβάμε μακριά από τον τοίχο με μικρή αλλά σταθερή ταχύτητα $\nu$. Η σανίδα θα αρχίσει να κινείται τόσο κατά τον οριζόντιο όσο και κατά τον κατακόρυφο άξονα, ενώ θα βρίσκεται σε επαφή με τον τοίχο και το έδαφος.
Θα αποδείξουμε πως το άνω άκρο της σανίδας θα καταλήξει να κινείται με άπειρη ταχύτητα. Προσπαθήστε να ανακαλύψετε σε ποιο από τα παρακάτω βήματα βρίσκεται το λάθος και γιατί.

ΑΠΟΔΕΙΞΗ

1. Ορίζουμε σαν $x(t)$ την οριζόντια απόσταση που απέχει κάθε χρονική στιγμή $t$ το κάτω άκρο της σανίδας από τον τοίχο.
2. Ορίζουμε σαν $y(t)$ την κάθετη απόσταση που απέχει κάθε χρονική στιγμή $t$ το άνω άκρο της σανίδας από το έδαφος.
3. Αφού ο τοίχος, το έδαφος και η σανίδα σχηματίζουν κάθε στιγμή ένα ορθογώνιο τρίγωνο, μπορούμε να γράψουμε:
$$L^2=x(t)^2+y(t)^2$$
4. Από το Βήμα 3 προκύπτει πως:
$$y(t)=\sqrt{L^2-x(t)^2}$$
5. Υπολογίζουμε την παράγωγο του $y$ ως προς $t$, με τον κανόνα της αλυσίδας και τον κανόνα της παραγώγισης σύνθετης συνάρτησης:
$$\frac{dy}{dt}=\frac{dy}{dx}\frac{dx}{dt}=\frac{-x}{\sqrt{L^2-x^2}}\frac{dx}{dt}$$
6. Το διαφορικό $dy/dt$ μπορούμε να το συμβολίσουμε σαν $u(t)$ και είναι η ταχύτητα που κινείται το άνω άκρο της σανίδας πάνω στον τοίχο και το διαφορικό $dx/dt$ είναι η σταθερή ταχύτητα $\nu$ που κινείται το κάτω άκρο της σανίδας πάνω στο έδαφος. Δηλαδή η σχέση στο Βήμα 5 γράφεται:
$$u(t)=\frac{-x(t)\cdot\nu}{\sqrt{L^2-x(t)^2}}$$ Στο ίδιο αποτέλεσμα θα καταλήγαμε και αν υπολογίζαμε την παράγωγο $dy/dt$ στον τύπο του 4ου Βήματος, αναλύοντας το $x(t)$ σε $x_o+\nu t$.
7. Όσο η σανίδα πλησιάζει να ακουμπήσει ολόκληρη στο έδαφος, το $x$ τείνει στο $L$. Έτσι ο αριθμητής του πιο πάνω κλάσματος τείνει στην τιμή $–L\nu$, η οποία είναι μη μηδενική και ο παρονομαστής τείνει στο μηδέν.
8. Άρα η ταχύτητα $u(t)$ του άνω άκρου της σανίδας συνεχώς αυξάνεται και ενώ η σανίδα τείνει να ακουμπήσει στο έδαφος, η ταχύτητα τείνει στο άπειρο.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Την παρακάτω απόδειξη πως είμαι ο Πάπας την έστειλα στο Βατικανό και περιμένω την απόφασή τους για το σχετικό χρίσμα. Λέτε να γίνει δεκτή ή όχι και γιατί;

1. Ξεκινάμε με την ισότητα $x^2=x\cdot x$
2. Το δεύτερο μέλος γράφεται $x+x+x+\ldots+x$   ($x$ φορές)
3. Άρα $x^2=x+x+x+\ldots+x$   ($x$ φορές)
4. Παίρνουμε την παράγωγο ως προς $x$ και των δύο μελών: $(x^2)'=(x+x+x+\ldots+x)'$
5. Επειδή η παράγωγος ενός αθροίσματος ισούται με το άθροισμα των παραγώγων του έχουμε: $(x^2)'=x'+x'+x'+\ldots+x'$
6. Υπολογίζουμε τις παραγώγους και στα δύο μέλη: $2x=1+1+1+\ldots+1$   ($x$ φορές)
7. Άρα $2x=x$
8. Για $x\neq 0$ προκύπτει πως $2=1$
9. Ο Πάπας είναι ένας.
10. Κι εγώ είμαι ένας.
11. Άρα εγώ και ο Πάπας είμαστε δύο.
12. Επειδή όμως στο Βήμα 8 απέδειξα πως $2=1$, σημαίνει πως εγώ και ο Πάπας είμαστε ένα.
13. Άρα εγώ είμαι ο Πάπας!

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Προσπαθήστε να βρείτε που βρίσκεται το λάθος στον παρακάτω υπολογισμό:

1. Έστω πως $x$ είναι το βάρος ενός ελέφαντα και $y$ είναι το βάρος ενός κουνουπιού.

2. Έστω πως $2b$ είναι το συνολικό τους βάρος. Δηλαδή $x+y=2b$

3. Την πιο πάνω εξίσωση μπορούμε να την γράψουμε με δύο τρόπους: Α) $x=\,–y+2b$     Β) $x–2b=\,–y$

4. Πολλαπλασιάζουμε κατά μέλη τις εξισώσεις Α και Β και παίρνουμε: $x(x–2b)=\,–y(–y+2b)\Leftrightarrow x^2–2xb=y^2–2yb$

5. Προσθέτουμε σε κάθε μέλος της πιο πάνω εξίσωσης το $b^2$ και έχουμε: $x^2–2xb+b^2=y^2–2yb+b^2$

6. Παραγοντοποιούμε και τα δύο μέλη με χρήση της γνωστής ταυτότητας: $(x–b)^2=(y–b)^2$

7. Παίρνουμε την τετραγωνική ρίζα και των δύο μελών: $x–b=y–b$

8. Προσθέτουμε το $b$ και στα δύο μέλη: $x=y$

και καταλήγουμε πως ένας ελέφαντας ζυγίζει όσο ένα κουνούπι!

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Παρακάτω θα αποδείξουμε πως κάθε φυσικός αριθμός μπορεί να προσδιορισθεί με δεκατέσσερις λέξεις ή λιγότερες. Φυσικοί λέγονται οι ακέραιοι αριθμοί που είναι μεγαλύτεροι του 0. Λέγοντας λέξεις εννοούμε ελληνικές λέξεις που περιέχονται σε οποιοδήποτε λεξικό και οι οποίες πρέπει να σχηματίζουν κάποια φράση με νόημα. Π.χ. η φράση "ο φυσικός αριθμός μεταξύ του τρία και του πέντε" προσδιορίζει τον αριθμό 4.
Η πρόταση είναι προφανώς εσφαλμένη για τον εξής λόγο: Οι ελληνικές λέξεις είναι πεπερασμένες. Οι συνδυασμοί που προκύπτουν από δεκατέσσερις λέξεις επιλεγμένες από ένα πεπερασμένο σύνολο λέξεων είναι επίσης πεπερασμένοι. Οι φυσικοί αριθμοί όμως είναι άπειροι και συνεπώς δεν μπορούν να αντιστοιχιστούν όλοι με κάποιον συνδυασμό 14 ή λιγότερων λέξεων, ακόμα και αν όλοι αυτοί οι συνδυασμοί είχαν κάποιο νόημα.

Η παρακάτω απόδειξη γίνεται με τη μέθοδο της ατόπου απαγωγής που λειτουργεί ως εξής: Θέλουμε να αποδείξουμε πως μία πρόταση Α είναι αληθής. Υποθέτουμε αρχικά πως είναι ψευδής και στη συνέχεια με λογικούς συνειρμούς προσπαθούμε να καταλήξουμε σε αντίφαση. Τότε η υπόθεση που κάναμε πως η πρόταση Α είναι ψευδής δεν είναι σωστή και συνεπώς η πρόταση Α πρέπει να είναι αληθής.
Προσπαθήστε να ανακαλύψετε γιατί η απόδειξη είναι λανθασμένη.

ΑΠΟΔΕΙΞΗ

1. Υποθέτουμε πως υπάρχουν φυσικοί αριθμοί που δεν μπορούν να προσδιορισθούν με δεκατέσσερις λέξεις ή λιγότερες.

2. Ένας από αυτούς τους αριθμούς θα είναι ο μικρότερος τους. Τον ονομάζουμε Ν.

3. Τότε ο αριθμός Ν μπορεί να ορισθεί ως «ο μικρότερος φυσικός αριθμός που δεν μπορεί να προσδιορισθεί με δεκατέσσερις λέξεις ή λιγότερες».

4. Αυτή η πρόταση προσδιορίζει τον αριθμό Ν με δεκατέσσερις λέξεις και άρα έρχεται σε αντίφαση με την υπόθεση πως ο Ν είναι ένας αριθμός που δεν μπορεί να προσδιορισθεί με δεκατέσσερις λέξεις ή λιγότερες.

5. Αφού η αρχική υπόθεση που κάναμε στο Βήμα 1 οδήγησε με λογικά βήματα σε αντίφαση, πρέπει να είναι εσφαλμένη.

6. Άρα όλοι οι φυσικοί αριθμοί μπορούν να προσδιορισθούν με δεκατέσσερις λέξεις ή λιγότερες!

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ