Γρίφοι Λογικής

Αταίριαστο σχήμα (***)

Ποιο από τα παρακάτω σχήματα ξεχωρίζει από τα υπόλοιπα;
Διευκρίνιση: Σαν σχήμα εννοούμε τη συνολική εικόνα και όχι μόνο το περίγραμμα.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Δύο παίκτες γράφουν διαδοχικά σε έναν πίνακα ακέραιους αριθμούς από το 1 έως το 1000. Οι κανόνες του παιχνιδιού απαγορεύουν να γράφονται στο πίνακα διαιρέτες των ήδη γραμμένων αριθμών. Χάνει ο παίκτης που δεν μπορεί να γράψει άλλον αριθμό. Ποιος από τους δύο παίκτες μπορεί να κερδίζει πάντοτε το παιχνίδι και γιατί;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Το διπλοκίνητο σκάκι είναι μια παραλλαγή του σκακιού στην οποία ο κάθε παίκτης παίζει δύο συνεχόμενες κινήσεις, αντί για μία που παίζει στο κλασικό σκάκι. Πρώτος παίζει ο λευκός. Με δεδομένο ότι και οι δύο παίκτες θα παίξουν τις καλύτερες δυνατές κινήσεις, μπορεί να κερδίζει ο μαύρος;
Υπόδειξη: Δεν χρειάζονται σκακιστικές γνώσεις για την επίλυση αυτού του γρίφου, εκτός από τον τρόπο με τον οποίο κινείται ο ίππος.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Τρεις φίλοι που βγαίνουν συχνά μαζί παραγγέλνουν είτε μπύρα είτε κρασί σύμφωνα με τους παρακάτω κανόνες:
- Αν ο Ανδρέας παραγγείλει μπύρα τότε ο Βλάσης παραγγέλνει ότι και ο Γιάννης.
- Αν ο Βλάσης παραγγείλει μπύρα τότε ο Ανδρέας και ο Γιάννης δίνουν διαφορετικές παραγγελίες.
- Αν ο Γιάννης παραγγείλει κρασί τότε ο Ανδρέας παραγγέλνει ότι και ο Βλάσης.
Ποιος παραγγέλνει πάντα το ίδιο ποτό και ποιο είναι αυτό;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ήτανε δυο νάνοι, ο Πέστο κι ο Ξαναπέστο. Ο Πέστο λέει ψέματα κάθε Δευτέρα, Τρίτη και Τετάρτη και τις υπόλοιπες μέρες λέει αλήθεια. Ο Ξαναπέστο λέει ψέματα κάθε Πέμπτη, Παρασκευή και Σάββατο και τις υπόλοιπες μέρες λέει αλήθεια. Μια μέρα που τους συνάντησα, μου είπαν τα εξής:
- Πέστο: Χθες έλεγα ψέματα.
- Ξαναπέστο: Το ίδιο κι εγώ.
Ποια μέρα συνάντησα τους δύο νάνους;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο Γιώργος κοιτάζει την Άννα και η Άννα κοιτάζει τον Νίκο. Ο Γιώργος φοράει γυαλιά και ο Νίκος δεν φοράει. Κοιτάζει κάποιος με γυαλιά κάποιον χωρίς γυαλιά; Επιλέξτε μία από τις πιο κάτω απαντήσεις και αιτιολογήστε την επιλογή σας:
Α) Ναι
Β) Όχι
Γ) Δεν μπορεί να προσδιοριστεί

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έχω τοποθετήσει σε ένα τραπέζι 3 τραπουλόχαρτα με την όψη τους κρυμμένη. Τα δύο είναι άσσοι και το τρίτο βαλές. Εσείς δεν ξέρετε τη ταυτότητα του καθενός, εγώ όμως την ξέρω. Σκοπός σας είναι να εντοπίσετε έναν άσσο. Για το σκοπό αυτό, έχετε μία και μόνη βοήθεια. Μπορείτε να δείξετε ένα φύλλο με το δάχτυλό σας και να μου κάνετε μία οποιαδήποτε ερώτηση που να απαντιέται μόνο με ναι ή όχι. Αν το φύλλο που δείχνει το δάχτυλο σας είναι άσσος, θα απαντήσω με ειλικρίνεια στην ερώτηση σας. Αν το φύλλο που δείχνει το δάχτυλο σας είναι ο βαλές θα απαντήσω τυχαία ναι ή όχι, ανεξάρτητα από την απάντηση που επιδέχεται η ερώτηση. Πώς θα τα καταφέρετε;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Στο σάκο του Αϊ-Βασίλη υπάρχουν 2015 δώρα, από τα οποία τα 1008 έχουν πράσινο περιτύλιγμα και τα 1007 κόκκινο περιτύλιγμα. Ο Αϊ-Βασίλης μοιράζει τα δώρα στα παιδιά ως εξής: Κάθε παιδί τραβάει στην τύχη από το σάκο 2 δώρα και α) αν είναι και τα δύο κόκκινα, ξαναβάζει το ένα στο σάκο και κρατάει το άλλο, β) αν είναι το ένα πράσινο και το άλλο κόκκινο, ξαναβάζει το πράσινο στο σάκο και κρατάει το κόκκινο, γ) αν είναι και τα δυο πράσινα, τα κρατάει και τα δύο και ο Αϊ-Βασίλης προσθέτει έναν ακόμη κόκκινο δώρο στο σάκο (από κάποιο εφεδρικό στοκ). Η διαδικασία αυτή επαναλαμβάνεται μέχρις ότου στο σάκο του Αϊ-Βασίλη απομείνει ένα μόνο δώρο. Ποια είναι η πιθανότητα αυτό να έχει κόκκινο περιτύλιγμα;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έξι φίλοι κάθονται σε μία καφετέρια. Έρχεται το γκαρσόνι, αλλά αντί να ρωτήσει ξεχωριστά τον καθένα τι θα παραγγείλει, τους κάνει τη γενική ερώτηση: «θα πιείτε όλοι καφέ;»
Οι 6 φίλοι απάντησαν με τη σειρά, ο καθένας τους με μία από τις φράσεις «ναι», «όχι», «δεν ξέρω» και κάποιος από αυτούς απάντησε σίγουρα «όχι». Το γκαρσόνι κατάλαβε ακριβώς πόσους καφέδες έπρεπε να φέρει μόνο αφού άκουσε και την απάντηση του τελευταίου.
Πόσους καφέδες έφερε και τι απάντησαν οι 6 φίλοι;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Η Ελένη θέλει ο άντρας που θα γνωρίσει να είναι ψηλός, λεπτός, μελαχρινός ή έστω να έχει όσο το δυνατόν περισσότερα από αυτά τα χαρακτηριστικά. Υποψήφιοι είναι ο Άρης, ο Βασίλης, ο Γιώργος και ο Δημήτρης. Γνωρίζουμε τα εξής για τους τέσσερις άντρες:

1. Ο καθένας τους διαθέτει διαφορετικό αριθμό των πιο πάνω επιθυμητών χαρακτηριστικών από τους άλλους.
2. Μόνο ένας από τους Άρη ή Δημήτρη είναι ψηλός και ξανθός.
3. Μόνο ένας από τους Βασίλη ή Γιώργο είναι κοντός και λεπτός.
4. Ο Δημήτρης και ο Γιώργος είναι είτε και οι δύο ψηλοί είτε και οι δύο κοντοί.
5. Ο Βασίλης και ο Άρης είναι είτε και οι δύο μελαχρινοί είτε και οι δύο ξανθοί.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Βρείτε τον αριθμό Ζ που προκύπτει από τις παρακάτω 10 προτάσεις:

1. Τουλάχιστον μία από τις προτάσεις 9 και 10 είναι αληθής.
2. Αυτή είναι είτε η πρώτη αληθής είτε η πρώτη ψευδής πρόταση.
3. Υπάρχουν τρεις διαδοχικές ψευδείς προτάσεις.
4. Η διαφορά μεταξύ των αριθμών της τελευταίας αληθούς και της πρώτης αληθούς πρότασης διαιρεί τον αριθμό Z.
5. Ο αριθμός Z είναι το άθροισμα των αριθμών όλων των αληθών προτάσεων.
6. Αυτή δεν είναι η τελευταία αληθής πρόταση.
7. Ο αριθμός κάθε αληθούς πρότασης διαιρεί τον αριθμό Z.
8. Ο αριθμός Z είναι το ποσοστό (%) των αληθών προτάσεων.
9. Το πλήθος των θετικών ακέραιων διαιρετών του αριθμού Z (χωρίς το 1 και τον Ζ) είναι μεγαλύτερο από το άθροισμα των αριθμών των αληθών προτάσεων.
10. Δεν υπάρχουν τρεις διαδοχικές αληθείς προτάσεις.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ο διευθυντής του φρενοκομείου στο Νησί των Καταραμένων κάλεσε τον αστυνόμο Σαΐνη για να διαλευκάνει μια δύσκολη υπόθεση. Στο ίδρυμά μας, του είπε, στεγάζονται μόνο γιατροί και ψυχικά διαταραγμένοι νοσηλευόμενοι. Τελευταία όμως όλοι έχουν αρχίσει να συμπεριφέρονται περίεργα. Τους παρατήρησα και κατάφερα να συγκεντρώσω τις πιο κάτω πληροφορίες:

1. Μερικοί έχουν γίνει δάσκαλοι των υπολοίπων. Ο καθένας έχει τουλάχιστον έναν δάσκαλο.
2. Κανένα άτομο Α δεν είναι διατεθειμένο να γίνει δάσκαλος ενός άλλου Β, εκτός αν ο Α πιστεύει ότι ο Β εμπιστεύεται τον εαυτό του.
3. Ο καθένας είτε εμπιστεύεται κάποιον είτε όχι.
4. Για κάθε άτομο Α υπάρχει ένα Β που εμπιστεύεται μόνο τα άτομα τα οποία έχουν τουλάχιστον έναν δάσκαλο που τον εμπιστεύεται ο Α. Με άλλα λόγια, για οποιοδήποτε άτομο Χ ισχύει ότι αν ο Α εμπιστεύεται κάποιον δάσκαλο του Χ τότε ο Β εμπιστεύεται τον Χ, αντίθετα αν ο Α δεν εμπιστεύεται κανέναν δάσκαλο του Χ, τότε ο Β δεν εμπιστεύεται τον Χ.
5. Υπάρχει κάποιος που εμπιστεύεται όλους τους νοσηλευόμενους αλλά δεν εμπιστεύεται κανέναν από τους γιατρούς.
6. Οι παράφρονες αντιλαμβάνονται τις σχέσεις εμπιστοσύνης όλων των υπολοίπων αντίθετα, ενώ οι υγιείς τις αντιλαμβάνονται σωστά.

Πράγματι, κάτι δεν πάει καθόλου καλά στο φρενοκομείο σας, συμπέρανε ο Σαΐνης. Είτε κάποιος από τους νοσηλευόμενους είναι υγιής και θα πρέπει να ελευθερωθεί, είτε κάποιος από τους γιατρούς είναι παράφρων και θα πρέπει να απολυθεί.
Πώς έφτασε ο αστυνόμος Σαΐνης σε αυτό το συμπέρασμα;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Ένας άγνωστος σε εμάς αριθμός Ν λογικολόγων πρόκειται να παίξουν το παρακάτω παιχνίδι: Ένας διαιτητής θα κολλήσει από δύο βούλες στο μέτωπο του κάθε λογικολόγου. Λέει σε όλους πως έχει στη διάθεσή του Ν+1 κόκκινες και Ν+1 μαύρες βούλες. Εκείνο που δεν ξέρουν είναι πως ο διαιτητής κόλλησε μία κόκκινη και μία μαύρη βούλα στο μέτωπο όλων των λογικολόγων εκτός από έναν στον οποίο κόλλησε δύο κόκκινες βούλες.
Οι λογικολόγοι κάθονται σε έναν κύκλο έτσι ώστε ο καθένας να βλέπει τις βούλες όλων των υπολοίπων. Ο διαιτητής τους ρωτάει με τη σειρά αρχίζοντας από αυτόν που κάθεται στη θέση 1, τι χρώμα έχουν οι δύο βούλες τους. Ο λογικολόγος με τις δύο κόκκινες βούλες κάθεται στην άγνωστη σε εμάς θέση Θ.
Για ποια Ν και για ποια Θ ο λογικολόγος με τις δύο κόκκινες βούλες καταφέρνει να βρει το χρώμα τους; Η απάντησή σας θα πρέπει να είναι αιτιολογημένη.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Έχουμε μια ορθογώνια διάταξη με τελείες τοποθετημένες σε ένα πλέγμα μ x ν (μ σειρές, ν στήλες) με μ ≠ ν και μ,ν > 2. Δύο παίκτες επιλέγουν εναλλάξ μία από τις απομένουσες κάθε φορά τελείες του πλέγματος και την αφαιρούν μαζί με όλες τις άλλες τελείες που βρίσκονται πάνω από αυτή και δεξιά της. Στόχος του κάθε παίκτη είναι να αναγκάσει τον αντίπαλο να αφαιρέσει την τελευταία τελεία.

Π.χ. έστω ένα πλέγμα της αρχικής μορφής 6 x 7 :

Αν ο πρώτος παίκτης επιλέξει την πέμπτη τελεία της τρίτης σειράς, θα αφήσει στον αντίπαλο την παρακάτω διάταξη:

Βρείτε ποιος από τους δύο παίκτες μπορεί στα σίγουρα να κερδίσει σε αυτό το παιχνίδι και εξηγήστε τον λόγο, χωρίς να απαιτείται να γνωρίζετε ούτε μία από τις κινήσεις που θα κάνει.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Παρακάτω θα αναφερθεί ένα σύντομο βιογραφικό της Μαρίνας. Στη συνέχεια θα σας δοθούν 4 πιθανά σημερινά επαγγέλματα και απασχολήσεις για τη Μαρίνα και θα πρέπει να τα κατατάξετε από το πιο πιθανό προς το πιο απίθανο. Προς αποφυγή σύγχυσης έχει αφαιρεθεί η επιλογή «Άνεργη».
Σωστές θα θεωρηθούν όλες οι κατατάξεις που δεν περιέχουν λογικά λάθη.

Η Μαρίνα είναι μία έξυπνη και δραστήρια γυναίκα ηλικίας 28 ετών σήμερα. Μετά το σχολείο σπούδασε κοινωνιολογία. Είναι πολύ επικοινωνιακή και εξωστρεφής. Ασχολήθηκε ενεργά με περιβαλλοντικά ζητήματα όπως η προστασία του περιβάλλοντος και η υπερθέρμανση του πλανήτη. Στα ενδιαφέροντά της συγκαταλέγονται θέματα ισότητας των δύο φύλων και δικαιωμάτων των γυναικών στον σύγχρονο κόσμο.

Τα 4 πιθανά επαγγέλματα – απασχολήσεις για τη Μαρίνα σήμερα είναι:
Α) Τραπεζική υπάλληλος
Β) Τραπεζική υπάλληλος και μέλος μιας φεμινιστικής οργάνωσης
Γ) Κοινωνική λειτουργός
Δ) Σύμβουλος ενεργειακής απόδοσης κτιρίων

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Σε ένα δωμάτιο υπάρχουν 10 άνθρωποι, όλοι διαφορετικού ύψους. Ο καθένας τους θέλει να κάνει από μία χειραψία μόνο με όσους είναι πιο κοντοί από αυτόν. Πόσες χειραψίες θα γίνουν συνολικά;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

Για την κούρσα των 400 μέτρων μιας αθλητικής διοργάνωσης δήλωσαν συμμετοχή 25 αθλητές. Ο στίβος διαθέτει 5 διαδρομές, οπότε μόνο 5 αθλητές μπορούν να αγωνίζονται ταυτόχρονα. Πόσες είναι οι λιγότερες κούρσες που πρέπει να γίνουν για να προσδιορισθούν οι 3 γρηγορότεροι αθλητές του συνόλου και να τους αποδοθούν το χρυσό, το αργυρό και το χάλκινο μετάλλιο; Ποιοι αθλητές θα τρέξουν σε κάθε κούρσα;

Σημειώσεις: Υποθέστε πως ο κάθε αθλητής έχει την ίδια απόδοση σε κάθε κούρσα. Τα αποτελέσματα των αγώνων βγαίνουν από τη σχετική κατάταξη των αθλητών και όχι από τους χρόνους τους. Δεν είναι απαραίτητο να εφαρμόσετε μια τυπική διαδικασία επιλογής αθλητών γιατί το ζητούμενο εδώ είναι μόνο να αναδειχτούν σωστά οι τρεις ταχύτεροι και όχι να κλιμακώνεται το ενδιαφέρον των αγώνων.

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ

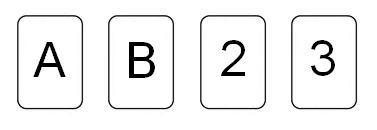
Κάποιος τοποθετεί τις 4 κάρτες που φαίνονται στο σχήμα πάνω σε ένα τραπέζι και ισχυρίζεται πως κάθε κάρτα που έχει φωνήεν από τη μία όψη της έχει ζυγό αριθμό από την άλλη.
Πόσες το πολύ και ποιες είναι οι κάρτες που πρέπει απαραιτήτως να αναποδογυρίσετε για να διαπιστώσετε αν ο ισχυρισμός του είναι σωστός;

Μόνο για Μέλη: στείλτε την απάντησή σας εδώ