Γρίφοι Ανάλυσης

Συνάντηση στη βιβλιοθήκη (***)

Κάποτε τρεις φίλοι συναντήθηκαν σε μία βιβλιοθήκη. Ο πρώτος είπε: «Στο εξής εγώ θα έρχομαι στη βιβλιοθήκη μόνο μέρα παρά μέρα». Ο δεύτερος δήλωσε ότι θα έρχεται στη βιβλιοθήκη κάθε τρίτη μέρα, ενώ ο τρίτος ότι θα έρχεται κάθε τέταρτη μέρα.
Ο βιβλιοθηκάριος που άκουσε τη συζήτηση, τους πληροφόρησε ότι κάθε Τετάρτη η βιβλιοθήκη παραμένει κλειστή. Οι φίλοι είπαν ότι, αν κάποιος επρόκειτο να έρθει στη βιβλιοθήκη τη μέρα που είναι κλειστή, θα έρθει την επόμενη μέρα και η αρχή μέτρησης των περαιτέρω επισκέψεών του θα γίνεται από τη μέρα εκείνη. Έτσι και έκαναν.
Μπορεί να συναντήθηκαν ξανά κάποια Δευτέρα στη βιβλιοθήκη; Αν ναι, ποια μέρα της εβδομάδας έγινε η συζήτηση; Αν όχι, γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Μπορούμε να γεμίσουμε ένα τετραγωνισμένο ταμπλό 10x10 τετραγώνων με τουβλάκια διαστάσεων 1x4; Αν ναι, πώς θα διατάξουμε τα τουβλάκια στα 16 κεντρικά τετράγωνα του ταμπλό; Αν όχι, γιατί;
Σημείωση: Όλα τα τουβλάκια πρέπει να βρίσκονται μέσα στο ταμπλό και δεν επιτρέπονται επικαλύψεις.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

100 παιδιά έχουν αρχικά από 100 καραμέλες το καθένα. Μερικά παιδιά μοίρασαν μία ή περισσότερες καραμέλες σε ένα ή περισσότερα από τα άλλα παιδιά και κάθε παιδί κατέληξε με θετικό αριθμό καραμελών, αλλά διαφορετικό από κάθε άλλο παιδί. Πόσα τουλάχιστον παιδιά μοίρασαν καραμέλες σε άλλα παιδιά;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Υπάρχει ένα κυκλικό τραπέζι με Θ θέσεις. Όταν 11 θέσεις του είναι πιασμένες, το τραπέζι δεν έχει γεμίσει αλλά κάθε ελεύθερη θέση του είναι δίπλα σε μία τουλάχιστον πιασμένη θέση.
Ποια είναι μικρότερη και ποια η μεγαλύτερη δυνατή τιμή του Θ;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ο Τρύφωνας πήρε δύο μικρούς κύβους και στον καθένα κόλλησε σε κάθε έδρα του έναν τυχαίο αριθμό από το 1 έως το 6, φτιάχνοντας έτσι δύο ζάρια με τυχαίους και πιθανώς επαναλαμβανόμενους αριθμούς στις έδρες τους. Παρατήρησε ότι όταν έριχνε μαζί τα δύο ζάρια, η πιθανότητα να φέρει το ζάρι Β μεγαλύτερο αριθμό από το το ζάρι Α ήταν μεγαλύτερη από 50%. Στη συνέχεια έφτιαξε με τον ίδιο τρόπο ένα ζάρι Γ το οποίο όταν το έριχνε μαζί με το ζάρι Β, η πιθανότητα να φέρει το ζάρι Γ μεγαλύτερο αριθμό από το ζάρι Β ήταν μεγαλύτερη από 50%.
Είναι δυνατόν αν ρίξει μαζί το ζάρι Α με το ζάρι Γ, η πιθανότητα να φέρει το ζάρι Α μεγαλύτερο αριθμό από το ζάρι Γ να είναι μεγαλύτερη από 50%; Αν ναι, δώστε ένα παράδειγμα. Αν όχι, γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Μια μέρα ένας εξωγήινος από έναν προηγμένο πολιτισμό επισκέφτηκε τη Γη για να συλλέξει πληροφορίες όσον αφορά την ανθρώπινη γνώση. Ο οικοδεσπότης του ήταν ο κ. Σμιθ, με τον οποίο έγινε ο εξής διάλογος:
- Σμιθ: Γιατί δεν παίρνεις μαζί σου την εγκυκλοπαίδεια «Μπριτάνικα»; Είναι σπουδαία περίληψη όλων των γνώσεων μας. Βέβαια, έχει αρκετά μεγάλο βάρος.
- Εξωγήινος: Πολύ καλή ιδέα. Αλλά δεν χρειάζεται να κουβαλήσω το βάρος της. Θα κωδικοποιήσω όλη την εγκυκλοπαίδεια πάνω σε αυτή τη μεταλλική ράβδο. Όλη τη δουλειά θα τη κάνει ένα σημαδάκι στη ράβδο.
- Σμιθ: Αστειεύεσαι φυσικά.
- Εξωγήινος: Καθόλου! Υπάρχουν λιγότερα από χίλια διαφορετικά γράμματα και σύμβολα στην εγκυκλοπαίδεια σας. Θα αντιστοιχίσω έναν αριθμό από το 1 έως το 999 στο κάθε γράμμα ή σύμβολο, προσθέτοντας μηδενικά στα αριστερά αν χρειαστεί, έτσι ώστε κάθε αριθμός που χρησιμοποιείται να έχει ακριβώς 3 ψηφία. Για παράδειγμα, η λέξη γάτα μπορεί να κωδικοποιηθεί ως 003001019001.
Χρησιμοποιώντας έναν πανίσχυρο υπολογιστή τσέπης, ο εξωγήινος αναπαράγει γρήγορα την εγκυκλοπαίδεια, κωδικοποιώντας ολόκληρο το περιεχόμενο της σε έναν τεράστιο αριθμό. Στη συνέχεια, τοποθέτησε υποδιαστολή μπροστά από τον αριθμό, και τον μετέτρεψε σε δεκαδικό. Ο εξωγήινος τοποθέτησε μετά ένα σημείο στη ράβδο του, χωρίζοντας την ακριβώς σε μήκη α και β, έτσι ώστε το κλάσμα α/β, να ισούται με το δεκαδικό αριθμό του κώδικα του.
- Εξωγήινος: Όταν γυρίσω στον πλανήτη μου, ένας από τους υπολογιστές μας, θα μετρήσει επακριβώς τα α και β και θα υπολογίσει το κλάσμα α/β. Ο αριθμός που θα προκύψει θα αποκωδικοποιήσει ολόκληρη την εγκυκλοπαίδεια σας.

Τι λέτε, θα μπορούσε ένας αρκούντως προηγμένος πολιτισμός να εφαρμόσει αυτήν την κωδικοποίηση;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

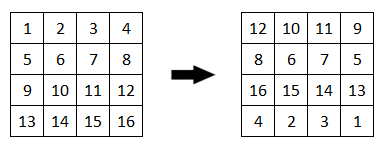
Μπορούμε να μετασχηματίσουμε τον αριστερό πίνακα στον δεξί, αντιμεταθέτοντας τις γραμμές και τις στήλες του; Αν ναι, ποιος είναι ο ελάχιστος αριθμός αντιμεταθέσεων; Αν όχι, γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Τριάντα άτομα κάθονται γύρω από ένα στρογγυλό τραπέζι. Καθένας από αυτούς είναι ή έξυπνος ή κουτός και όλοι διαδοχικά απαντούν στην ερώτηση: "τι είναι αυτός που κάθεται δεξιά σου, έξυπνος ή κουτός;". Ένας έξυπνος απαντάει πάντα σωστά, ενώ ένας κουτός άλλοτε σωστά και άλλοτε όχι. Εσείς το μόνο που ξέρετε είναι ότι οι κουτοί δεν υπερβαίνουν κάποιον αριθμό. Ποια είναι η μέγιστη δυνατή τιμή αυτού του αριθμού, ώστε έχοντας ακούσει όλες τις απαντήσεις να είστε σε θέση να εντοπίσετε με βεβαιότητα έναν τουλάχιστον έξυπνο; Αιτιολογήστε.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Η Άννα, η Βίκυ και η Γιάννα έχουν βγει για χριστουγεννιάτικα ψώνια. Στη βιτρίνα ενός μαγαζιού υπάρχουν 5 είδη από ζευγάρια σκουλαρίκια. Η τιμή του κάθε ζευγαριού είναι ακέραιος αριθμός, διαφορετικός για κάθε ζευγάρι. Η Άννα αγόρασε 4 από τα 5 ζευγάρια και πλήρωσε 21 ευρώ. Η Βίκυ αγόρασε 3 ζευγάρια και πλήρωσε 23 ευρώ.
Αν η Γιάννα αγόρασε και τα 5, ποιο ήταν το ελάχιστο και ποιο το μέγιστο ποσό που πλήρωσε;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Δύο φίλοι παίζουν το εξής παιχνίδι: Ο πρώτος θα πει έναν αριθμό από το 1 έως το 10. Ο δεύτερος θα αυξήσει τον αριθμό του πρώτου κατά 1 έως 10 μονάδες και αυτό θα συνεχιστεί εναλλάξ μέχρι ο ένας από τους δύο να πει τον αριθμό 50 και να κερδίσει. Ποιος από τους δύο παίκτες μπορεί να κερδίζει πάντα το παιχνίδι και ποιον αριθμό πρέπει να πει την πρώτη φορά που θα παίξει;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

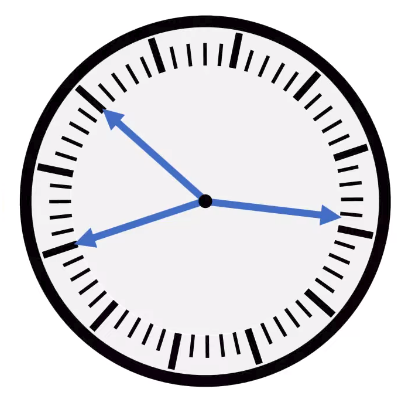
Ο Λουκάς, όσο περίμενε τη σειρά του στο ΚΕΠ, χάζευε το ρολόι στον τοίχο που φαίνεται στην εικόνα. Δεν είχε αριθμούς πάνω του και θα μπορούσε να είναι περιστραμμένο γύρω από τον άξονά του. Επίσης οι δείκτες των ωρών, των λεπτών και των δευτερολέπτων είχαν όλοι το ίδιο μήκος. Λειτουργούσε πάντως σαν κανονικό ρολόι. Τι ώρα ήταν;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Πέντε φίλοι επισκέφτηκαν μία Ελληνική ταβέρνα για φαγητό. Ο ιδιοκτήτης τους δείχνει τον κατάλογο με τα 10 πιάτα του μενού και επειδή του είπαν πως τους αρέσουν οι γρίφοι, τους βάζει την ακόλουθη πρόκληση: Μπορούν να παραγγείλουν ένα πιάτο του μενού ο καθένας, όχι όμως με την περιγραφή του καταλόγου αλλά με έναν κωδικό από το Α έως το Κ που ο ιδιοκτήτης έχει αντιστοιχίσει μυστικά στα 10 πιάτα. Μόλις ο ιδιοκτήτης πάρει την παραγγελία των 5 πιάτων τα ετοιμάζει και τα τοποθετεί στο κέντρο του τραπεζιού έτσι ώστε να μην προκύπτει ποιος κωδικός αντιστοιχεί σε ποιο πιάτο. Τους είπε πως αν καταφέρουν μετά από 3 συνεχόμενες ημέρες επανάληψης της ίδιας διαδικασίας να του αντιστοιχίσουν σωστά τα 10 πιάτα με τους 10 κωδικούς, τότε θα τους κεράσει και τις 3 ημέρες του φαγητού τους. Ποιες πρέπει να είναι οι παραγγελίες των 5 φίλων κάθε μία από τις 3 ημέρες ώστε να φάνε δωρεάν;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ο Φαραώ Amenhotep ο 2ος κάλεσε μια μέρα τον Sennefer, τον σοφό του παλατιού, και του ζήτησε να γράψει σε έναν πάπυρο 20 θετικούς ρητούς αριθμούς της επιλογής του, όχι απαραίτητα διαφορετικούς μεταξύ τους, τους οποίους δεν θα γνώριζε ο φαραώ. Στη συνέχεια ο Sennefer θα δώσει στον φαραώ μια λίστα διακριτών αριθμών, καθένας από τους οποίους πρέπει να είναι ένας ή το άθροισμα περισσότερων του ενός από τους αριθμούς που έγραψε στον πάπυρο.
Στη συνέχεια ο φαραώ διαβάζοντας τους αριθμούς της λίστας θα προσπαθήσει να βρει τους 20 αριθμούς που έγραψε ο σοφός στον πάπυρο. Αν ο φαραώ καταφέρει να βρει δύο ή περισσότερες ομάδες των 20 αριθμών από τις οποίες προκύπτουν οι αριθμοί της λίστας, τότε θα πάρει το κεφάλι του σοφού. Αν από τους αριθμούς της λίστας προκύπτουν με έναν και μοναδικό τρόπο οι 20 αριθμοί του πάπυρου, τότε θα πάρει από το κεφάλι του σοφού μία τρίχα για κάθε αριθμό της λίστας ώστε να τις προσθέσει στην ψεύτικη γενειάδα του.
Πόσες τουλάχιστον τρίχες πρέπει να θυσιάσει ο σοφός για να γλυτώσει το κεφάλι του;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Η θέση του διαγράμματος έχει προκύψει από μία κανονική παρτίδα σκάκι και είναι η σειρά του μαύρου να παίξει. Μπορείτε να βρείτε μία κίνηση που έχουν κάνει οπωσδήποτε τα μαύρα σε αυτήν την παρτίδα; (κομμάτι που κινήθηκε, αρχικό τετράγωνο, τελικό τετράγωνο).

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Έχουμε σε ένα χαρτί τις κορυφές ενός κανονικού πολυγώνου και θέλουμε να τις ενώσουμε για να φτιάξουμε ένα αστέρι. Ο τρόπος κατασκευής του αστεριού είναι ο εξής: Ξεκινάμε από μία οποιαδήποτε κορυφή και την ενώνουμε με κάποια άλλη κορυφή, εκτός της διπλανής της, με φορά προς τα δεξιά. Στη συνέχεια την κορυφή που καταλήξαμε την ενώνουμε με την επόμενη κατάλληλη κορυφή προς τα δεξιά, φροντίζοντας πάντα ο αριθμός των κορυφών που βρίσκονται ανάμεσα στις δύο τελευταίες γραμμές που τραβήξαμε να είναι ο ίδιος. Στο τέλος πρέπει να καταλήξουμε στην αρχική μας κορυφή, έχοντας όμως ενώσει όλες τις κορυφές του πολυγώνου.
Έτσι προκύπτει ότι υπάρχει ένας τρόπος για να φτιάξουμε αστέρι εάν έχουμε 5 κορυφές, κανένας τρόπος για να φτιάξουμε αστέρι εάν έχουμε 6 κορυφές και 2 τρόποι για να φτιάξουμε αστέρι εάν έχουμε 7 κορυφές. Με πόσους τρόπους μπορούμε να φτιάξουμε αστέρι εάν έχουμε 2000 κορυφές;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ο Αντώνης και ο Βασίλης έχουν αγοράσει ένα κυκλικό ταψάκι με γαλακτομπούρεκο και ετοιμάζονται να το μοιράσουν μεταξύ τους με τον εξής τρόπο:
Ο Αντώνης κόβει το γαλακτομπούρεκο κατά μήκος μιας ευθείας γραμμής. Χωρίς να αφαιρεθεί κομμάτι από το ταψάκι, ο Βασίλης κάνει και αυτός μία ευθεία τομή. Ο Αντώνης κάνει ακόμα μία ευθεία τομή και τέλος ο Βασίλης κάνει μία τέταρτη και τελευταία ευθεία τομή.
Στη συνέχεια παίρνουν εναλλάξ από ένα κομμάτι ο καθένας, ξεκινώντας από τον Αντώνη. Υπάρχει στρατηγική κοψίματος για κάποιον από τους δύο φίλους ώστε να φάει περισσότερο ή ίσο γαλακτομπούρεκο σε σχέση με τον άλλον;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Θέλουμε να μετακινήσουμε τον ίππο που βρίσκεται στο τετράγωνο h1 της εικόνας έτσι ώστε να περάσει διαδοχικά μόνο μία φορά από όλα τα τετράγωνα της σκακιέρας (εκτός από το τμήμα που λείπει) και να επιστρέψει στην αρχική του θέση. Είναι δυνατόν να τα καταφέρουμε; Αν ναι, δώστε ένα παράδειγμα χρησιμοποιώντας τις συντεταγμένες της εικόνας. Αν όχι, αιτιολογήστε την απάντησή σας.
Σημείωση: Ο ίππος κινείται όπως στο σκάκι, δηλαδή κάνει ένα "Γ" προς οποιαδήποτε κατεύθυνση.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Η Ένωση Αντικοινωνικών Ελλάδος (Ε.Α.Ε.) μετά το ετήσιο συνέδριό της, συναντιέται κάθε χρόνο στο μπαρ Μονόχνωτος για ποτό, το οποίο και κλείνει αποκλειστικά για τα μέλη της. Σε αυτό το μπαρ υπάρχουν 25 σκαμπό σε μία σειρά, αριθμημένα από το 1 έως το 25. Τα μέλη της έρχονται το καθένα μόνο του και κάθονται διαδοχικά στα σκαμπό του μπαρ. Το κάθε μέλος κάθεται όσο πιο μακριά γίνεται από τα υπόλοιπα μέλη που κάθονται ήδη και σε καμία περίπτωση δεν κάθεται δίπλα σε άλλο μέλος.
Στον ιδιοκτήτη του μπαρ όμως δεν αρέσει να έχει κενά σκαμπό γιατί έτσι πουλάει λιγότερα ποτά. Φέτος λοιπόν σκέφτηκε έναν τρόπο για να κάτσουν όσο το δυνατόν περισσότερα μέλη στο μπαρ του. Πρότεινε λοιπόν στον πρώτο αντικοινωνικό που μπήκε να κάτσει σε μια συγκεκριμένη θέση. Ποια θέση του πρότεινε;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

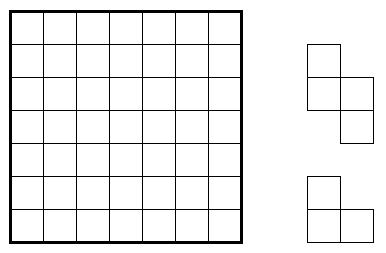
Θέλουμε να γεμίσουμε το πλέγμα των 49 τετραγώνων με τα δύο είδη πλακιδίων που φαίνονται στην εικόνα. Το κάθε πλακίδιο μπορεί να χρησιμοποιηθεί πολλές φορές και μπορεί να περιστραφεί ή να αναποδογυριστεί εάν χρειάζεται, δεν επιτρέπεται όμως να βγαίνει εκτός του πλέγματος, ούτε να επικαλύπτονται τα πλακίδια.
Είναι δυνατόν να καταφέρουμε το ζητούμενο; Αν ναι, ποιος είναι ο ελάχιστος αριθμός πλακιδίων που μπορούμε να χρησιμοποιήσουμε; Αν όχι, γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ρίχνουμε ένα κομμάτι παγωμένου λαδιού μέσα σε ένα ποτήρι με νερό. Περιμένουμε να ισορροπήσει και σημειώνουμε το ύψος της στάθμης του νερού. Όταν λιώσει το παγωμένο λάδι, η στάθμη του νερού θα μειωθεί, θα παραμείνει ίδια, ή θα αυξηθεί σε σχέση με πριν και γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

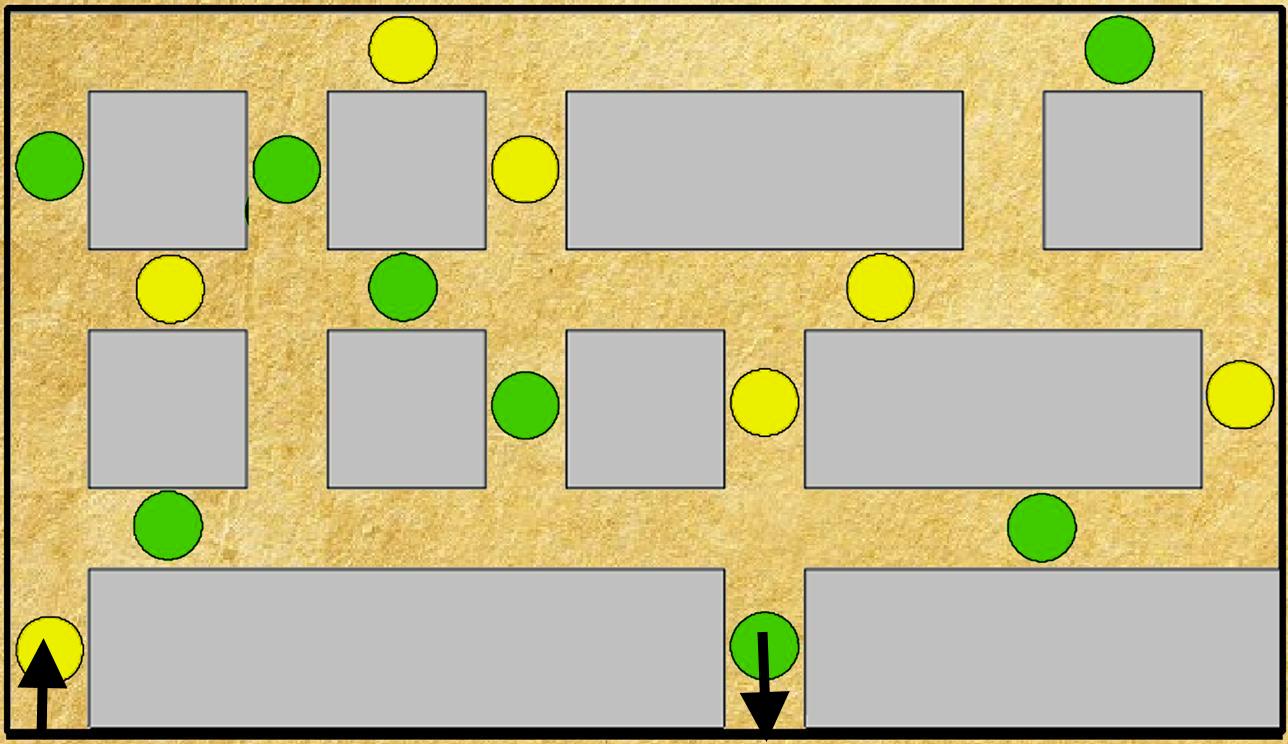
Στον λαβύρινθο της εικόνας πρέπει να εισέλθουμε από το βέλος πριν τον κίτρινο κύκλο και να εξέλθουμε από το βέλος μετά τον πράσινο κύκλο. Μπορούμε να περάσουμε από τον κάθε κύκλο όσες φορές θέλουμε ή και καμία, αλλά πάντοτε πρέπει να περνάμε εναλλάξ τους κίτρινους και τους πράσινους κύκλους.
Είναι δυνατόν να ολοκληρωθεί η διαδρομή σύμφωνα με τους παραπάνω κανόνες; Αν ναι, πόσες είναι οι ελάχιστες φορές που θα χρειαστεί να περάσουμε από κάθε χρώμα και αν όχι, γιατί;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Πέντε άδεια δοχεία ίσης χωρητικότητας βρίσκονται σε μια κυκλική διάταξη και δύο παίχτες, ο Α και ο Β, παίζουν ένα παιχνίδι σε διαδοχικούς γύρους. Πρώτος παίζει ο Α, που με μια κανάτα παίρνει 1 λίτρο νερό από μια βρύση και το μοιράζει όπως θέλει στα πέντε δοχεία. Ο Β με τη σειρά του επιλέγει δυο γειτονικά δοχεία, τα αδειάζει στο νεροχύτη και τα ξαναβάζει στην θέση τους. Το ίδιο γίνεται και σε κάθε επόμενο γύρο. Σκοπός του Α είναι να ξεχειλίσει σε κάποιον γύρο τουλάχιστον ένα από τα πέντε δοχεία, ενώ σκοπός του Β είναι να μην το επιτρέψει.
Ποια είναι η ελάχιστη χωρητικότητα των δοχείων για να έχει ο Β νικητήρια στρατηγική; Δώστε ένα παράδειγμα μιας τέτοιας στρατηγικής για τον Β με τη χωρητικότητα που βρήκατε και δώστε ένα παράδειγμα μιας στρατηγικής του Α που κερδίζει σε οποιαδήποτε μικρότερη χωρητικότητα από αυτή που βρήκατε.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Ο λύκος στο τετράγωνο ζ1 της εικόνας προσπαθεί να φτάσει τα πρόβατα της 8ης γραμμής και ο βοσκός στο τετράγωνο ε7 προσπαθεί να τον εμποδίσει. Ο λύκος και ο βοσκός κινούνται εναλλάξ και σε κάθε κίνησή τους μετακινούνται σε ένα από τα γειτονικά τους τετράγωνα, συμπεριλαμβανομένων και των διαγώνιων γειτονικών τετραγώνων. Ο βοσκός μπορεί να κινηθεί και στα τετράγωνα των προβάτων, δηλαδή από την αρχική του θέση μπορεί να κινηθεί σε 8 τετράγωνα. Τα πρόβατα δεν μετακινούνται. Αν ο λύκος πέσει πάνω στον βοσκό τον τρώει και στη συνέχεια φτάνει τα πρόβατα, ενώ αν ο βοσκός πέσει πάνω στον λύκο τον σκοτώνει και ησυχάζει. Πρώτος κινείται ο λύκος. Θα καταφέρει να φάει έστω και ένα πρόβατο ή μπορεί ο βοσκός με τις κατάλληλες κινήσεις να τον εμποδίσει; Δικαιολογήστε την απάντησή σας με κάποιες από τις καλύτερες κινήσεις και για τους δύο πάνω στο διάγραμμα, χρησιμοποιώντας τις συντεταγμένες που δίνονται.

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Δύο φοιτητές μαθηματικών παίζουν το παρακάτω παιχνίδι: Ο πρώτος βάζει στο μυαλό του ένα νούμερο από το 0 έως το 2000 και ο δεύτερος πρέπει να το μαντέψει με όσο το δυνατόν λιγότερες προσπάθειες. Ο τρόπος εύρεσης του νούμερου είναι ο εξής: Ο δεύτερος κάνει μία ερώτηση και ο πρώτος απαντάει αποκλειστικά με μία από τις λέξεις "μεγαλύτερο" ή "μικρότερο" ή "ίσο". Η λέξη που επιλέγεται από τον πρώτο παίκτη πρέπει να απαντά ειλικρινά και με σαφήνεια στην ερώτηση που τίθεται. Αν η ερώτηση δεν επιδέχεται μία σαφή απάντηση εκ των τριών που δίνονται, τότε ο δεύτερος παίκτης χάνει την πρόκληση. Κάθε νέα ερώτηση που γίνεται θεωρείται μια νέα προσπάθεια. Ποιος είναι ο ελάχιστος αριθμός προσπαθειών που απαιτείται για να βρει ο δεύτερος παίκτης το νούμερο, όσο άτυχος και αν φανεί στις απαντήσεις που θα πάρει και ποιες ερωτήσεις πρέπει να κάνει;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ

Δύο τυφλοί βρέθηκαν σε ένα εμπορικό κέντρο και ο καθένας τους αγόρασε ένα ζευγάρι άσπρες και δύο ζευγάρια μαύρες κάλτσες, όλες ίδιες μεταξύ τους εκτός από το χρώμα τους. Στο δρόμο προς το σπίτι τους συγκρούστηκαν μεταξύ τους και τα 6 ζευγάρια καλτσών σκορπίστηκαν στο έδαφος. Ευτυχώς το κάθε ζευγάρι παρέμεινε ενωμένο γιατί οι δύο κάλτσες του συγκρατούνταν μεταξύ τους με ένα μανταλάκι.
Οι δύο τυφλοί όμως δεν έχασαν την ψυχραιμία τους και παρόλο που δεν είχαν κανέναν να τους βοηθήσει, κατάφεραν να γυρίσει ο καθένας σπίτι του έχοντας μαζί του τις κάλτσες που ήθελε. Τι έκαναν;

Μόνο για Μέλη: Στείλτε την απάντησή σας εδώ